RL Parallel Circuit (Impedance, Phasor Diagram)

Regarding the RL parallel circuit, this article will explain the information below.

• Equation, magnitude, vector diagram, and impedance phase angle of RL parallel circuit impedance

Impedance of the RL parallel circuit

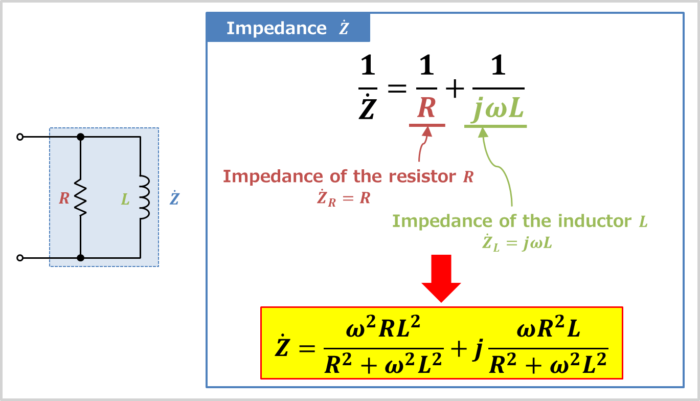
An RL parallel circuit (also known as an RL filter or RL network) is an electrical circuit consisting of a resistor \(R\) and an inductor \(L\) connected in parallel, driven by a voltage source or current source.

The impedance \({\dot{Z}}_R\) of the resistor \(R\) and the impedance \({\dot{Z}}_L\) of the inductor \(L\) can be expressed by the following equations:

\begin{eqnarray}
{\dot{Z}}_R&=&R\tag{1}\\
\\
{\dot{Z}}_L&=&jX_L=j{\omega}L\tag{2}
\end{eqnarray}

,where \({\omega}\) is the angular frequency, which is equal to \(2{\pi}f\), and \(X_L\left(={\omega}L\right)\) is called inductive reactance, which is the resistive component of inductor \(L\).

The sum of the reciprocals of each impedance is the reciprocal of the impedance \({\dot{Z}}\) of the RL parallel circuit. Therefore, it can be expressed by the following equation:

\begin{eqnarray}
\frac{1}{{\dot{Z}}}&=&\frac{1}{{\dot{Z}_R}}+\frac{1}{{\dot{Z}_L}}\\
\\
&=&\frac{1}{R}+\frac{1}{j{\omega}L}\\
\\
&=&\frac{j{\omega}L}{R×j{\omega}L}+\frac{R}{R×j{\omega}L}\\
\\
&=&\frac{R+j{\omega}L}{j{\omega}RL}\tag{3}
\end{eqnarray}

From equation (3), by interchanging the denominator and numerator, the following equation is obtained:

\begin{eqnarray}
{\dot{Z}}=\frac{1}{\displaystyle\frac{1}{R}+\displaystyle\frac{1}{j{\omega}L}}=\frac{j{\omega}RL}{R+j{\omega}L}\tag{4}
\end{eqnarray}

From equation (4), there is an imaginary unit \(j\) in the denominator and numerator. To make sure that only the numerator has an imaginary unit \(j\), multiply the denominator and numerator by "\(R-j{\omega}L\)".

\begin{eqnarray}
{\dot{Z}}&=&\frac{j{\omega}RL(R-j{\omega}L)}{(R+j{\omega}L)(R-j{\omega}L)}\\
\\
&=&\frac{j{\omega}R^2L-j^2{\omega}^2RL^2}{R^2-j{\omega}RL+j{\omega}RL-j^2{\omega}^2L^2}\\
\\
&=&\frac{j{\omega}R^2L+{\omega}^2RL^2}{R^2+{\omega}^2L^2}\\
\\
&=&\frac{{\omega}^2RL^2}{R^2+{\omega}^2L^2}+j\frac{{\omega}R^2L}{R^2+{\omega}^2L^2}\tag{5}
\end{eqnarray}

From the above, the impedance \({\dot{Z}}\) of the RL parallel circuit can be expressed as:

Magnitude of the impedance of the RL parallel circuit

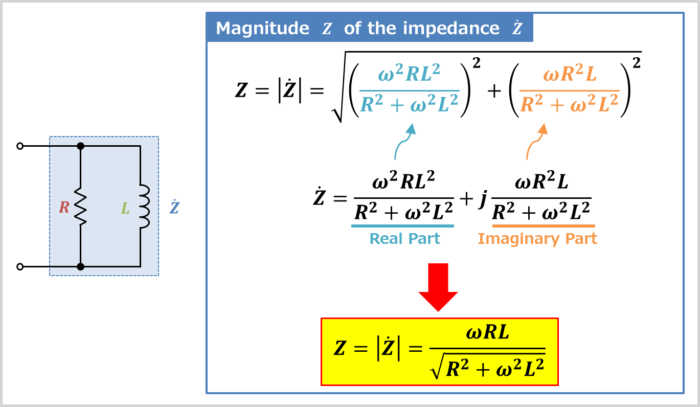
We have just obtained the impedance \({\dot{Z}}\) expressed by the following equation.

\begin{eqnarray}
{\dot{Z}}=\frac{{\omega}^2RL^2}{R^2+{\omega}^2L^2}+j\frac{{\omega}R^2L}{R^2+{\omega}^2L^2}{\mathrm{[{\Omega}]}}\tag{7}
\end{eqnarray}

The magnitude \(Z\) of the impedance of the RL parallel circuit is the absolute value of the impedance \({\dot{Z}}\) in equation (7).

In more detail, the magnitude \(Z\) of the impedance \({\dot{Z}}\) can be obtained by adding the square of the real part \(\displaystyle\frac{{\omega}^2RL^2}{R^2+{\omega}^2L^2}\) and the square of the imaginary part \(\displaystyle\frac{{\omega}R^2L}{R^2+{\omega}^2L^2}\) and taking the square root, which can be expressed in the following equation:

\begin{eqnarray}
Z&=&|{\dot{Z}}|\\
\\
&=&\displaystyle\sqrt{\left(\displaystyle\frac{{\omega}^2RL^2}{R^2+{\omega}^2L^2}\right)^2+\left(\displaystyle\frac{{\omega}R^2L}{R^2+{\omega}^2L^2}\right)^2}\\
\\
&=&\displaystyle\sqrt{\displaystyle\frac{{\omega}^4R^2L^4+{\omega}^2R^4L^2}{\left(R^2+{\omega}^2L^2\right)^2}}\\
\\
&=&\displaystyle\sqrt{\displaystyle\frac{{\omega}^2R^2L^2\left({\omega}^2L^2+R^2\right)}{\left(R^2+{\omega}^2L^2\right)^2}}\\
\\
&=&\displaystyle\sqrt{\displaystyle\frac{{\omega}^2R^2L^2}{R^2+{\omega}^2L^2}}\\
\\
&=&\displaystyle\frac{{\omega}RL}{\displaystyle\sqrt{R^2+{\omega}^2L^2}}\\
\\
&=&\displaystyle\frac{1}{\displaystyle\sqrt{\left(\displaystyle\frac{1}{R}\right)^2+\left(\displaystyle\frac{1}{{\omega}L}\right)^2}}\tag{8}
\end{eqnarray}

From the above, the magnitude \(Z\) of the impedance of the RL parallel circuit can be expressed as:

Vector diagram of the RL parallel circuit

The vector diagram of the impedance \({\dot{Z}}\) of the RL parallel circuit can be drawn in the following steps.

Let's take a look at each step in turn.

Draw the vector of impedance \({\dot{Z}_{RE}}\) of the real part of impedance \({\dot{Z}}\)

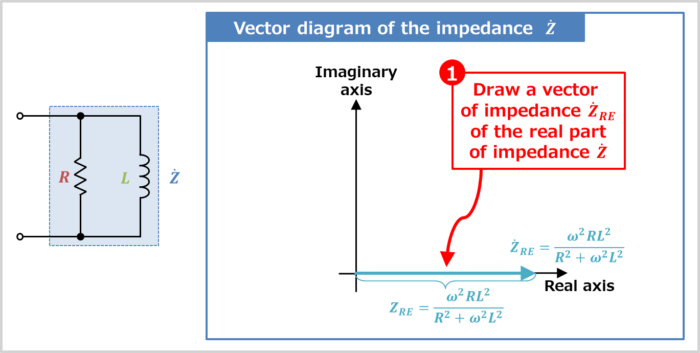
The impedance \({\dot{Z}_{RE}}\) of the real part of impedance \({\dot{Z}}\) is expressed by:

\begin{eqnarray}
{\dot{Z}_{RE}}=\frac{{\omega}^2RL^2}{R^2+{\omega}^2L^2}\tag{10}
\end{eqnarray}

Therefore, the vector direction of the impedance \({\dot{Z}_{RE}}\) is the direction of the real axis. How to determine the vector orientation will be explained in more detail later.

The magnitude (length) \(Z_{RE}\) of the vector of impedances \({\dot{Z}_{RE}}\) of the real part is given by

\begin{eqnarray}
Z_{RE}=|{\dot{Z}_{RE}}|=\displaystyle\sqrt{\left(\frac{{\omega}^2RL^2}{R^2+{\omega}^2L^2}\right)^2}=\frac{{\omega}^2RL^2}{R^2+{\omega}^2L^2}\tag{11}
\end{eqnarray}

Draw the vector of impedance \({\dot{Z}_{IM}}\) of the imaginary part of impedance \({\dot{Z}}\)

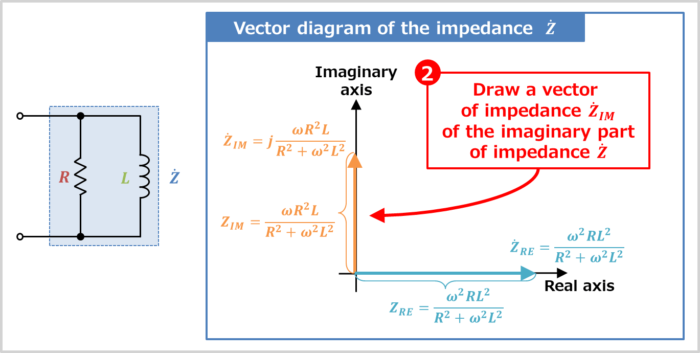
The impedance \({\dot{Z}_{IM}}\) of the imaginary part of impedance \({\dot{Z}}\) is expressed by:

\begin{eqnarray}
{\dot{Z}_{IM}}=j\frac{{\omega}R^2L}{R^2+{\omega}^2L^2}\tag{12}
\end{eqnarray}

Therefore, the vector direction of the impedance \({\dot{Z}_{IM}}\) is 90° counterclockwise around the real axis (with "\(+j\)", it rotates 90° counterclockwise). How to determine the vector orientation will be explained in more detail later.

The magnitude (length) \(Z_{IM}\) of the vector of impedances \({\dot{Z}_{IM}}\) of the imaginary part is given by

\begin{eqnarray}
Z_{IM}=|{\dot{Z}_{IM}}|=\displaystyle\sqrt{\left(\frac{{\omega}R^2L}{R^2+{\omega}^2L^2}\right)^2}=\frac{{\omega}R^2L}{R^2+{\omega}^2L^2}\tag{13}
\end{eqnarray}

Combine the vectors

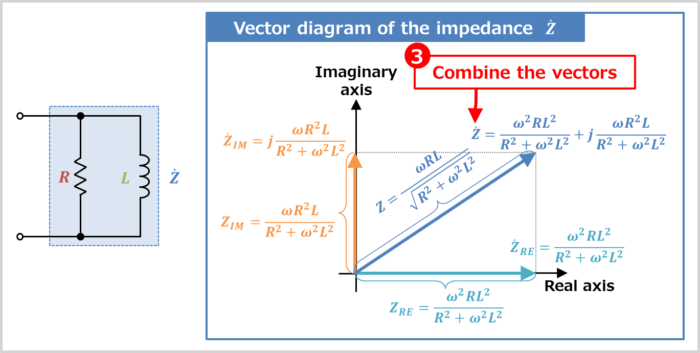
Combining the vector of "impedance \({\dot{Z}}_{RE}\) of the real part" and "impedance \({\dot{Z}}_{IM}\) of the imaginary part" is the vector diagram of the impedance \({\dot{Z}}\) of the RL parallel circuit.

The magnitude (length) \(Z\) of the vector of impedance \({\dot{Z}}\) of an RL parallel circuit is expressed by:

\begin{eqnarray}
Z=|{\dot{Z}}|=\displaystyle\frac{{\omega}RL}{\displaystyle\sqrt{R^2+{\omega}^2L^2}}=\displaystyle\frac{1}{\displaystyle\sqrt{\left(\displaystyle\frac{1}{R}\right)^2+\left(\displaystyle\frac{1}{{\omega}L}\right)^2}}{\mathrm{[{\Omega}]}}\tag{14}
\end{eqnarray}

Vector orientation

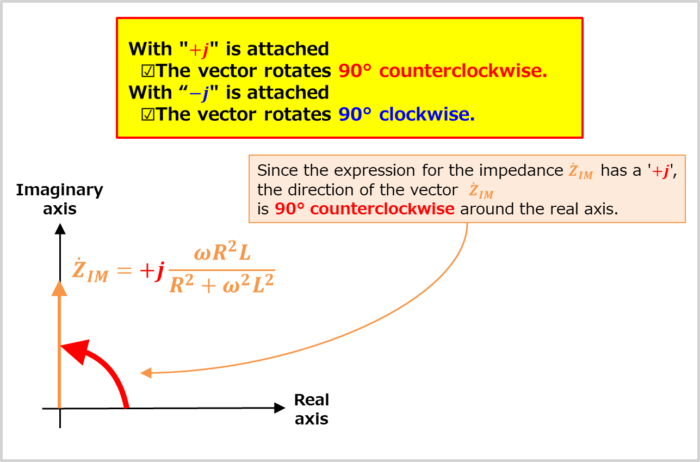
Here is a more detailed explanation of how vector orientation is determined.

The impedance \({\dot{Z}}_{IM}\) of the imaginary part of impedance \({\dot{Z}}\) is expressed by

\begin{eqnarray}
{\dot{Z}_{IM}}=j\frac{{\omega}R^2L}{R^2+{\omega}^2L^2}\tag{15}
\end{eqnarray}

Since the expression for the impedance \({\dot{Z}}_{IM}\) in the imaginary part has a "\(+j\)", the direction of the vector \({\dot{Z}}_{IM}\) is 90° counterclockwise around the real axis.

Impedance phase angle of the RL parallel circuit

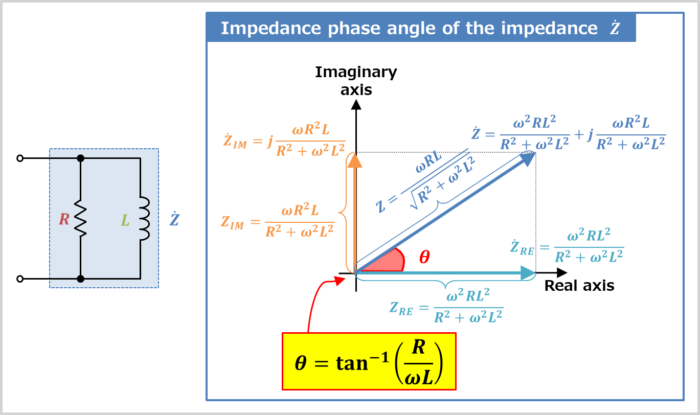
The impedance phase angle \({\theta}\) of the RL parallel circuit can be obtained from the vector diagram.

The impedance phase angle \({\theta}\) of the RL parallel circuit is expressed by the following equation:

\begin{eqnarray}
{\tan}{\theta}&=&\displaystyle\frac{\displaystyle\frac{{\omega}R^2L}{R^2+{\omega}^2L^2}}{\displaystyle\frac{{\omega}^2RL^2}{R^2+{\omega}^2L^2}}\\
\\
&=&\frac{R}{{\omega}L}\\
\\
{\Leftrightarrow}{\theta}&=&{\tan}^{-1}\left(\frac{R}{{\omega}L}\right)\\
\\
&=&{\tan}^{-1}\left(\frac{R}{{\omega}L}\right)\tag{16}
\end{eqnarray}

Summary

In this article, the following information on "RL parallel circuit was explained.

1. Equation, magnitude, vector diagram, and impedance phase angle of RL parallel circuit impedance

Thank you for reading.