Regarding the Resistor, this article will explain the information below.
- Rated Voltage
- Maximum Working Voltage
Rated Voltage and Maximum Working Voltage
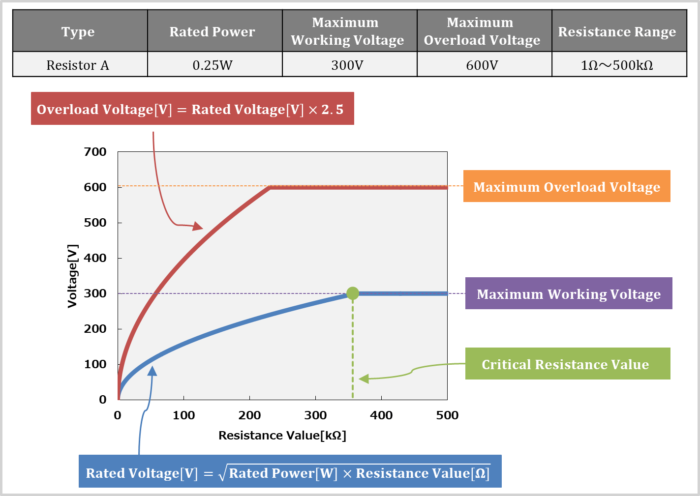
The data sheet of a resistor lists the rated power, maximum working voltage, and resistance range as shown in the figure above.
The rated voltage of a resistor is the maximum value of DC or AC voltage (RMS value) that can be continuously applied to the resistor.
The rated voltage can be calculated using the rated power and the resistance value, and is expressed by the following equation:
\begin{eqnarray}
\mbox{Rated Voltage}{\mathrm{[V]}}=\sqrt{\mbox{Rated Power}{\mathrm{[W]}}×\mbox{Resistance Value}{\mathrm{[{\Omega}]}}}
\end{eqnarray}
From the above equation, the larger the resistance value, the larger the rated voltage. The relationship between resistance value and rated voltage is shown by the blue line in the figure above.
The above figure shows that the rated voltage is constant after a certain value. This constant voltage is called the maximum working voltage.
The larger the resistance value of a resistor, the larger the voltage that can be continuously applied to the resistor. If the voltage applied to the resistor is very large, a short circuit may occur between the electrodes of the resistor, or the resistor may not be able to withstand the voltage, resulting in dielectric breakdown. For this reason, the upper limit of the voltage that can be continuously applied to a resistor is determined.
The resistance value at which the rated voltage equals the maximum working voltage is called the critical resistance value. If the resistance value of is less than the critical resistance value, the voltage can be continuously applied up to the rated voltage, and if the resistance value is greater than the critical resistance value, the voltage can be continuously applied up to the maximum working voltage.
In the data sheet shown earlier, the critical resistance value can be expressed by the following equation:
\begin{eqnarray}
\mbox{Critical Resistance Value}{\mathrm{[{\Omega}]}}=\frac{\mbox{Maximum Working Voltage}{\mathrm{[V]}}^2}{\mbox{Rated Voltage}{\mathrm{[W]}}}=\frac{300^2}{0.25}=360{\mathrm{[k{\Omega}]}}
\end{eqnarray}
Summary
This article described the following information about "Resistor".
- Rated Voltage
- Maximum Working Voltage
Thank you for reading.