Regarding the RC parallel circuit, this article will explain the information below.
- Equation, magnitude, vector diagram, and impedance phase angle of RC parallel circuit impedance
Iimpedance of the RC parallel circuit
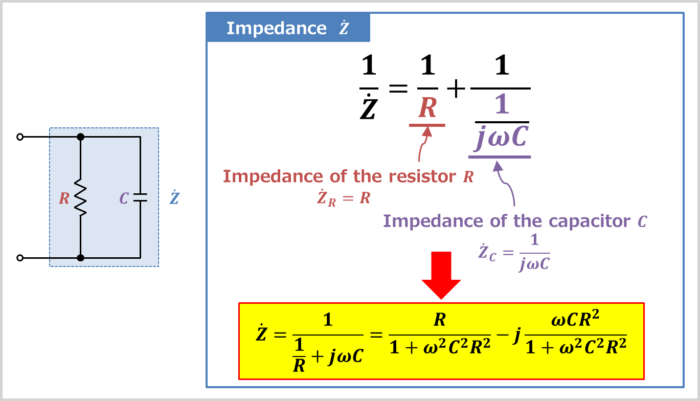
An RC parallel circuit (also known as an RC filter or RC network) is an electrical circuit consisting of a resistor \(R\) and a capacitor \(C\) connected in parallel, driven by a voltage source or current source.
The impedance \({\dot{Z}}_R\) of the resistor \(R\) and the impedance \({\dot{Z}}_C\) of capacitor \(C\) can be expressed by the following equations:
\begin{eqnarray}
{\dot{Z}_R}&=&R\tag{1}\\
\\
{\dot{Z}_C}&=&-jX_C=-j\frac{1}{{\omega}C}=\frac{1}{j{\omega}C}\tag{2}
\end{eqnarray}
,where \({\omega}\) is the angular frequency, which is equal to \(2{\pi}f\), and \(X_C\left(=\displaystyle\frac{1}{{\omega}C}\right)\) is called capacitive reactance, which is the resistive component of capacitor \(C\).
The sum of the reciprocals of each impedance is the reciprocal of the impedance \({\dot{Z}}\) of the RC parallel circuit. Therefore, it can be expressed by the following equation:
\begin{eqnarray}
\frac{1}{{\dot{Z}}}&=&\frac{1}{{\dot{Z}_R}}+\frac{1}{{\dot{Z}_C}}\\
\\
&=&\frac{1}{R}+\frac{1}{\displaystyle\frac{1}{j{\omega}C}}\\
\\
&=&\frac{1}{R}+j{\omega}C\\
\\
&=&\frac{1+j{\omega}CR}{R}\tag{3}
\end{eqnarray}
From equation (3), by interchanging the denominator and numerator, the following equation is obtained:
\begin{eqnarray}
{\dot{Z}}=\frac{1}{\displaystyle\frac{1}{R}+j{\omega}C}=\frac{R}{1+j{\omega}CR}\tag{4}
\end{eqnarray}
From equation (4), there is an imaginary unit \(j\) in the denominator. To make sure that only the numerator has an imaginary unit \(j\), multiply the denominator and numerator by "\(1-j{\omega}CR\)".
\begin{eqnarray}
{\dot{Z}}&=&\frac{R(1-j{\omega}CR)}{(1+j{\omega}CR)(1-j{\omega}CR)}\\
\\
&=&\frac{R-j{\omega}CR^2}{1-j{\omega}CR+j{\omega}CR-j^2{\omega}^2C^2R^2}\\
\\
&=&\frac{R-j{\omega}CR^2}{1+{\omega}^2C^2R^2}\\
\\
&=&\frac{R}{1+{\omega}^2C^2R^2}-j\frac{{\omega}CR^2}{1+{\omega}^2C^2R^2}\tag{5}
\end{eqnarray}
From the above, the impedance \({\dot{Z}}\) of the RC parallel circuit can be expressed as:
The impedance of the RC parallel circuit
\begin{eqnarray}
{\dot{Z}}=\frac{1}{\displaystyle\frac{1}{R}+j{\omega}C}=\frac{R}{1+{\omega}^2C^2R^2}-j\frac{{\omega}CR^2}{1+{\omega}^2C^2R^2}{\mathrm{[{\Omega}]}}\tag{6}
\end{eqnarray}
Magnitude of the impedance of the RC parallel circuit
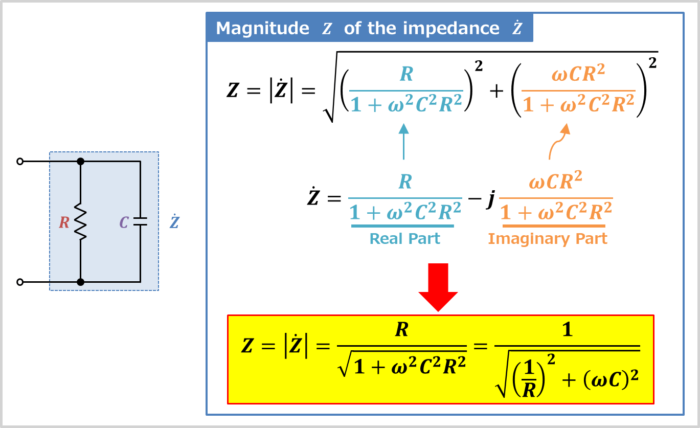
We have just obtained the impedance \({\dot{Z}}\) expressed by the following equation.
\begin{eqnarray}
{\dot{Z}}=\frac{R}{1+{\omega}^2C^2R^2}-j\frac{{\omega}CR^2}{1+{\omega}^2C^2R^2}{\mathrm{[{\Omega}]}}\tag{7}
\end{eqnarray}
The magnitude \(Z\) of the impedance of the RC parallel circuit is the absolute value of the impedance \({\dot{Z}}\) in equation (7).
In more detail, the magnitude \(Z\) of the impedance \({\dot{Z}}\) can be obtained by adding the square of the real part \(\displaystyle\frac{R}{1+{\omega}^2C^2R^2}\) and the square of the imaginary part \(\displaystyle\frac{{\omega}CR^2}{1+{\omega}^2C^2R^2}\) and taking the square root, which can be expressed in the following equation:
\begin{eqnarray}
Z&=&|{\dot{Z}}|\\
\\
&=&\displaystyle\sqrt{\left(\displaystyle\frac{R}{1+{\omega}^2C^2R^2}\right)^2+\left(\displaystyle\frac{{\omega}CR^2}{1+{\omega}^2C^2R^2}\right)^2}\\
\\
&=&\displaystyle\sqrt{\displaystyle\frac{R^2+{\omega}^2C^2R^4}{\left(1+{\omega}^2C^2R^2\right)^2}}\\
\\
&=&\displaystyle\sqrt{\displaystyle\frac{R^2\left(1+{\omega}^2C^2R^2\right)}{\left(1+{\omega}^2C^2R^2\right)^2}}\\
\\
&=&\displaystyle\sqrt{\displaystyle\frac{R^2}{1+{\omega}^2C^2R^2}}\\
\\
&=&\displaystyle\frac{R}{\displaystyle\sqrt{1+{\omega}^2C^2R^2}}\\
\\
&=&\displaystyle\frac{1}{\displaystyle\sqrt{\left(\displaystyle\frac{1}{R}\right)^2+\left({\omega}C\right)^2}}\tag{8}
\end{eqnarray}
From the above, the magnitude \(Z\) of the impedance of the RC parallel circuit can be expressed as:
The magnitude of the impedance of the RC parallel circuit
\begin{eqnarray}
Z=|{\dot{Z}}|=\displaystyle\frac{R}{\displaystyle\sqrt{1+{\omega}^2C^2R^2}}=\displaystyle\frac{1}{\displaystyle\sqrt{\left(\displaystyle\frac{1}{R}\right)^2+\left({\omega}C\right)^2}}{\mathrm{[{\Omega}]}}\tag{9}
\end{eqnarray}
Supplement
Some impedance \(Z\) symbols have a ". (dot)" above them and are labeled \({\dot{Z}}\).
\({\dot{Z}}\) with this dot represents a vector.
If it has a dot (e.g. \({\dot{Z}}\)), it represents a vector (complex number), and if it does not have a dot (e.g. \(Z\)), it represents the absolute value (magnitude, length) of the vector.
Vector diagram of the RC parallel circuit
The vector diagram of the impedance \({\dot{Z}}\) of the RC parallel circuit can be drawn in the following steps.
How to draw a Vector Diagram
- Draw the vector of impedance \({\dot{Z}_{RE}}\) of the real part of impedance \({\dot{Z}}\)
- Draw the vector of impedance \({\dot{Z}_{IM}}\) of the imaginary part of impedance \({\dot{Z}}\)
- Combine the vectors
Let's take a look at each step in turn.
Draw the vector of impedance \({\dot{Z}_{RE}}\) of the real part of impedance \({\dot{Z}}\)
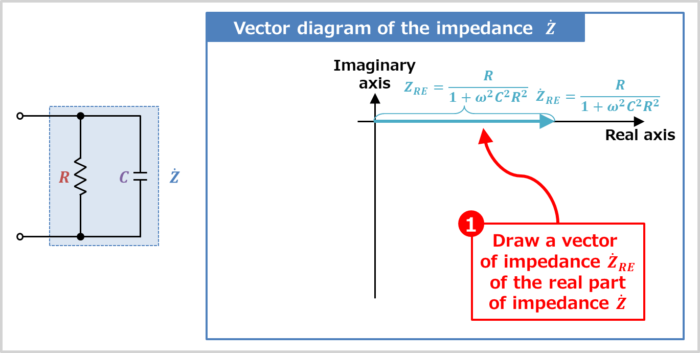
The impedance \({\dot{Z}_{RE}}\) of the real part of impedance \({\dot{Z}}\) is expressed by:
\begin{eqnarray}
{\dot{Z}_{RE}}=\frac{R}{1+{\omega}^2C^2R^2}\tag{10}
\end{eqnarray}
Therefore, the vector direction of the impedance \({\dot{Z}_{RE}}\) is the direction of the real axis. How to determine the vector orientation will be explained in more detail later.
The magnitude (length) \(Z_{RE}\) of the vector of impedances \({\dot{Z}_{RE}}\) of the real part is given by
\begin{eqnarray}
Z_{RE}=|{\dot{Z}_{RE}}|=\displaystyle\sqrt{\left(\frac{R}{1+{\omega}^2C^2R^2}\right)^2}=\frac{R}{1+{\omega}^2C^2R^2}\tag{11}
\end{eqnarray}
Draw the vector of impedance \({\dot{Z}_{IM}}\) of the imaginary part of impedance \({\dot{Z}}\)
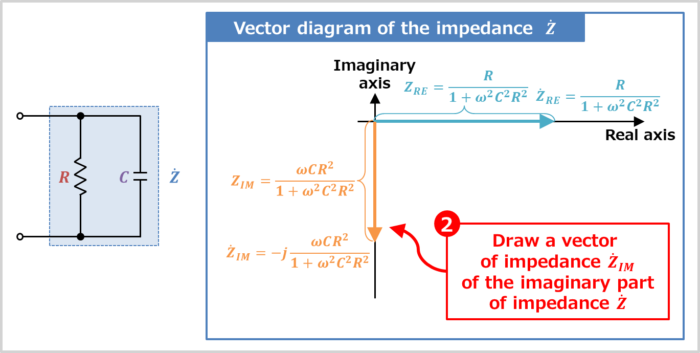
The impedance \({\dot{Z}_{IM}}\) of the imaginary part of impedance \({\dot{Z}}\) is expressed by:
\begin{eqnarray}
{\dot{Z}_{IM}}=-j\frac{{\omega}CR^2}{1+{\omega}^2C^2R^2}\tag{12}
\end{eqnarray}
Therefore, the vector direction of the impedance \({\dot{Z}_{IM}}\) is 90° clockwise around the real axis (with "\(-j\)", it rotates 90° clockwise). How to determine the vector orientation will be explained in more detail later.
The magnitude (length) \(Z_{IM}\) of the vector of impedances \({\dot{Z}_{IM}}\) of the imaginary part is given by
\begin{eqnarray}
Z_{IM}=|{\dot{Z}_{IM}}|=\displaystyle\sqrt{\left(\frac{{\omega}CR^2}{1+{\omega}^2C^2R^2}\right)^2}=\frac{{\omega}CR^2}{1+{\omega}^2C^2R^2}\tag{13}
\end{eqnarray}
Combine the vectors
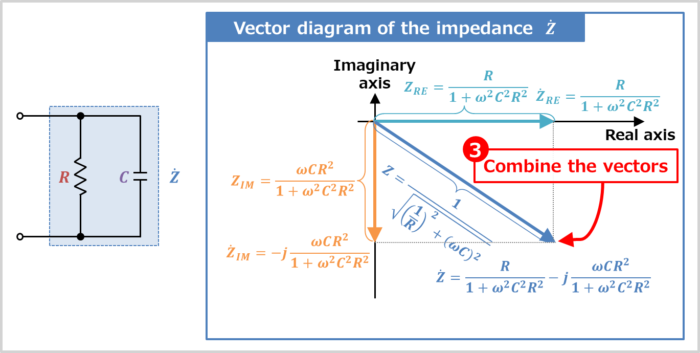
Combining the vector of "impedance \({\dot{Z}}_{RE}\) of the real part" and "impedance \({\dot{Z}}_{IM}\) of the imaginary part" is the vector diagram of the impedance \({\dot{Z}}\) of the RC parallel circuit.
The magnitude (length) \(Z\) of the vector of impedance \({\dot{Z}}\) of an RC parallel circuit is expressed by:
\begin{eqnarray}
Z=|{\dot{Z}}|=\displaystyle\frac{R}{\displaystyle\sqrt{1+{\omega}^2C^2R^2}}=\displaystyle\frac{1}{\displaystyle\sqrt{\left(\displaystyle\frac{1}{R}\right)^2+\left({\omega}C\right)^2}}{\mathrm{[{\Omega}]}}\tag{14}
\end{eqnarray}
Supplement
The magnitude (length) \(Z\) of the vector of the impedance \({\dot{Z}}\) of the RC parallel circuit can also be obtained using the Pythagorean theorem in the vector diagram.
Vector orientation
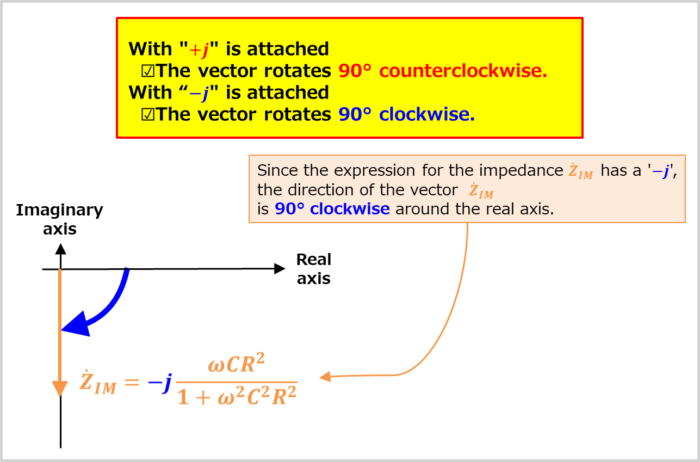
Here is a more detailed explanation of how vector orientation is determined.
Vector orientation
When an imaginary unit "\(j\)" is added to the expression, the direction of the vector is rotated by 90°.
- With "\(+j\)" is attached
- The vector rotates 90° counterclockwise.
- With "\(-j\)" is attached
- The vector rotates 90° clockwise.
The impedance \({\dot{Z}}_{IM}\) of the imaginary part of impedance \({\dot{Z}}\) is expressed by
\begin{eqnarray}
{\dot{Z}_{IM}}=-j\frac{{\omega}CR^2}{1+{\omega}^2C^2R^2}\tag{15}
\end{eqnarray}
Since the expression for the impedance \({\dot{Z}}_{IM}\) in the imaginary part has a "\(-j\)", the direction of the vector \({\dot{Z}}_{IM}\) is 90° clockwise around the real axis.
Impedance phase angle of the RC parallel circuit
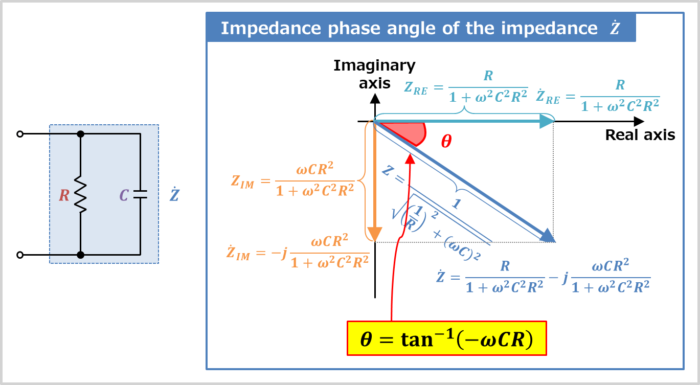
The impedance phase angle \({\theta}\) of the RC parallel circuit can be obtained from the vector diagram.
The impedance phase angle \({\theta}\) of the RC parallel circuit is expressed by the following equation:
\begin{eqnarray}
{\tan}{\theta}&=&\displaystyle\frac{-\displaystyle\frac{{\omega}CR^2}{1+{\omega}^2C^2R^2}}{\displaystyle\frac{R}{1+{\omega}^2C^2R^2}}\\
\\
&=&-{\omega}CR\\
\\
{\Leftrightarrow}{\theta}&=&{\tan}^{-1}\left(-{\omega}CR\right)\\
\\
&=&-{\tan}^{-1}\left({\omega}CR\right)\tag{16}
\end{eqnarray}
Summary
In this article, the following information on "RC parallel circuit was explained.
- Equation, magnitude, vector diagram, and impedance phase angle of RC parallel circuit impedance
Thank you for reading.
Related article
Related articles on impedance in series and parallel circuits are listed below. If you are interested, please check the link below.
- RL Series Circuit (Impedance, Phasor Diagram)
- RC Series Circuit (Impedance, Phasor Diagram)
- LC Series Circuit (Impedance, Phasor Diagram)
- RLC Series Circuit (Impedance, Phasor Diagram)
- RL Parallel Circuit (Impedance, Phasor Diagram)
- LC Parallel Circuit (Impedance, Phasor Diagram)
- RLC Parallel Circuit (Impedance, Phasor Diagram)