Q Factor of RLC Series Resonant Circuit

Regarding the Q Factor of RLC Series Resonant Circuit, this article will explain the information below.

• What is the Q factor of RLC series resonant circuit?
• Derivation of Q factor of RLC series resonant circuit
• Relationship between "Q factor" and "voltage across the inductor L and capacitor C

What is the Q factor of RLC series resonant circuit?

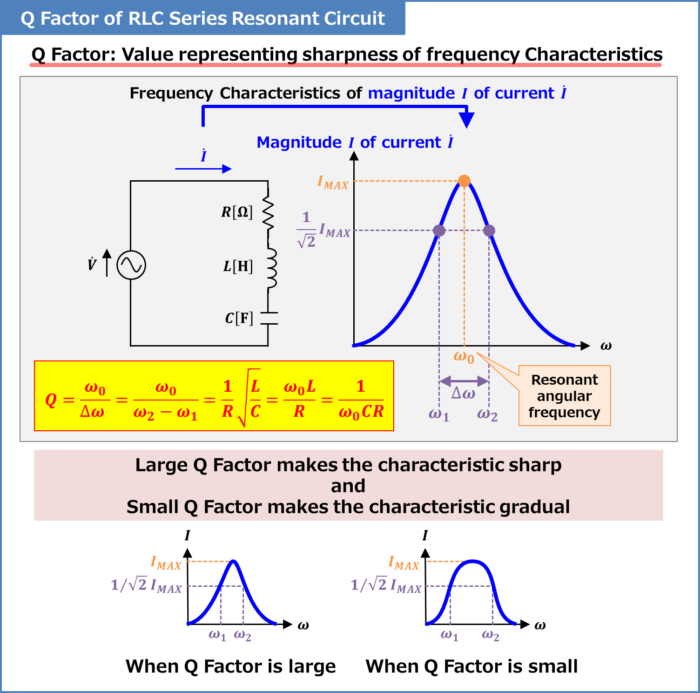
Q factor is a value that expresses the sharpness of the frequency characteristics. A large Q factor makes the frequency characteristics sharper, while a small Q factor makes the frequency characteristics more gradual.

The above figure shows the frequency characteristics of the magnitude $I$ of the current flowing in an RLC series resonant circuit. The RLC series resonant circuit is a circuit consisting of a resistor $R$, an inductor $L$, and a capacitor $C$ connected in series, and the magnitude $I$ of current reaches its maximum value $I_{MAX}$ at the angular frequency ${\omega}_0\left(=\displaystyle\frac{1}{\sqrt{LC}}\right)$ where the inductor $L$ and capacitor $C$ resonate.

In an RLC series resonant circuit, the Q factor is expressed by the following equation (the derivation of the following equation will be explained later).

In the above equation, ${\omega}_0$ is the resonant angular frequency, ${\omega}_1$ and ${\omega}_2$ are the angular frequencies when the magnitude $I$ of the current flowing in the RLC series resonant circuit is $\displaystyle\frac{1}{\sqrt{2}}$ times the magnitude of $I_{MAX}$ (${\omega}_1{<}{\omega}_2$), $R$ is the resistance of the resistor, $L$ is the inductance of the inductor, and $C$ is the capacitance of the capacitor.

From equation (1), the smaller ${\Delta}{\omega}(={\omega}_2-{\omega}_1)$ (the sharper the frequency response), the larger the Q factor.

Derivation of Q factor of RLC series resonant circuit

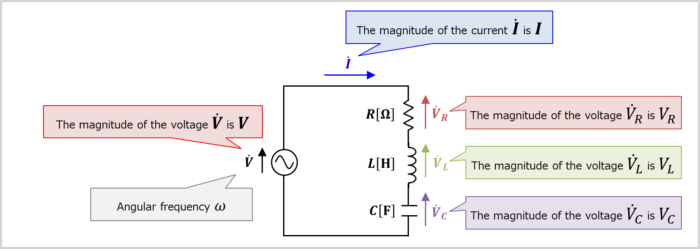
The RLC resonant series circuit is an electrical circuit consisting of a resistor $R$, an inductor $L$, and a capacitor $C$ connected in series.

When the resistance of resistor $R$ is $R{\mathrm{[{\Omega}]}}$, the inductance of inductor $L$ is $L{\mathrm{[H]}}$, and the capacitance of capacitor $C$ is $C{\mathrm{[F]}}$, the impedance ${\dot{Z}}$ of the RLC series resonant circuit becomes the following equation.

$$\begin{eqnarray} {\dot{Z}}=R+j\left({\omega}L-\frac{1}{{\omega}C}\right)\tag{2} \end{eqnarray}$$

, where ${\omega}$ is the angular frequency, which is equal to $2{\pi}f$.

The magnitude $Z$ of the impedance of the RLC series resonant circuit is expressed by the following equation.

$$\begin{eqnarray} Z=|{\dot{Z}}|=\sqrt{R^2+\left({\omega}L-\displaystyle\frac{1}{{\omega}C}\right)^2}\tag{3} \end{eqnarray}$$

Therefore, when the magnitude of the supply voltage is $V$, the magnitude $I$ of the current flowing in the RLC series resonant circuit is expressed by the following equation.

$$\begin{eqnarray} I=\frac{V}{Z}=\frac{V}{\sqrt{R^2+\left({\omega}L-\displaystyle\frac{1}{{\omega}C}\right)^2}}\tag{4} \end{eqnarray}$$

At the angular frequency (resonant angular frequency) )${\omega}_0\left(=\displaystyle\frac{1}{\sqrt{LC}}\right)$, the inductor $L$ and the capacitor $C$ are in resonance, and the following equation holds.

$$\begin{eqnarray} {\omega}_0&=&\frac{1}{\sqrt{LC}}\\ \\ {\Leftrightarrow}{{\omega}_0}^2&=&\frac{1}{LC}\\ \\ {\Leftrightarrow}{{\omega}_0}L&=&\frac{1}{{{\omega}_0}C}\\ \\ {\Leftrightarrow}{{\omega}_0}L-\frac{1}{{{\omega}_0}C}&=&0\tag{5} \end{eqnarray}$$

At resonant angular frequency ${\omega}_0$, the magnitude $I$ of the current flowing in the RLC series circuit is the maximum value $I_{MAX}$. $I_{MAX}$ is expressed by the following equation.

$$\begin{eqnarray} I_{MAX}&=&\frac{V}{\sqrt{R^2+\left({\omega}_0L-\displaystyle\frac{1}{{\omega}_0C}\right)^2}}\\ \\ &=&\frac{V}{\sqrt{R^2+0^2}}\\ \\ &=&\frac{V}{R}\tag{6} \end{eqnarray}$$

From equations (4) and (6), we obtain the following equation.

$$\begin{eqnarray} \frac{I}{I_{MAX}}&=&\frac{\displaystyle\frac{V}{\sqrt{R^2+\left({\omega}L-\displaystyle\frac{1}{{\omega}C}\right)^2}}}{\displaystyle\frac{V}{R}}\\ \\ &=&\frac{R}{\sqrt{R^2+\left({\omega}L-\displaystyle\frac{1}{{\omega}C}\right)^2}}\\ \\ &=&\frac{1}{\sqrt{1+\left(\displaystyle\frac{{\omega}L}{R}-\displaystyle\frac{1}{{\omega}CR}\right)^2}}\tag{7} \end{eqnarray}$$

Here, when "the magnitude $I$ of the current flowing in the RLC series resonance circuit" is $\displaystyle\frac{1}{\sqrt{2}}$ times "the magnitude $I_{MAX}$ of the current flowing at resonance" (when $I=\displaystyle\frac{1}{\sqrt{2}}I_{MAX}$), the following equation is obtained.

$$\begin{eqnarray} \frac{\displaystyle\frac{1}{\sqrt{2}}I_{MAX}}{I_{MAX}}&=&\frac{1}{\sqrt{1+\left(\displaystyle\frac{{\omega}L}{R}-\displaystyle\frac{1}{{\omega}CR}\right)^2}}\\ \\ {\Leftrightarrow}\frac{1}{\sqrt{2}}&=&\frac{1}{\sqrt{1+\left(\displaystyle\frac{{\omega}L}{R}-\displaystyle\frac{1}{{\omega}CR}\right)^2}}\\ \\ {\Leftrightarrow}\frac{{\omega}L}{R}-\frac{1}{{\omega}CR}&=&±1\tag{8} \end{eqnarray}$$

By using equation (8), the angular frequency ${\omega}$ can be obtained for the "Case $\displaystyle\frac{{\omega}L}{R}-\displaystyle\frac{1}{{\omega}CR}=1$" and the "Case $\displaystyle\frac{{\omega}L}{R}-\displaystyle\frac{1}{{\omega}CR}=-1$".

Case $\displaystyle\frac{{\omega}L}{R}-\displaystyle\frac{1}{{\omega}CR}=1$

Transforming "$\displaystyle\frac{{\omega}L}{R}-\displaystyle\frac{1}{{\omega}CR}=1$", we obtain the following equation.

$$\begin{eqnarray} \displaystyle\frac{{\omega}L}{R}-\displaystyle\frac{1}{{\omega}CR}=1\\ \\ {\Leftrightarrow}LC{\omega}^2-RC{\omega}-1=0\tag{9} \end{eqnarray}$$

Solving equation (9), the angular frequency ${\omega}$ is expressed by the following equation.

$$\begin{eqnarray} {\omega}=\frac{RC+\sqrt{(RC)^2+4LC}}{2LC}\tag{10} \end{eqnarray}$$

In the above equation, the root (√) is preceded by "+ (plus)" because ${\omega}{>}0$ is considered. Let ${\omega}$ in equation (10) be ${\omega}_2$.

Case $\displaystyle\frac{{\omega}L}{R}-\displaystyle\frac{1}{{\omega}CR}=-1$

Transforming "$\displaystyle\frac{{\omega}L}{R}-\displaystyle\frac{1}{{\omega}CR}=-1$", we obtain the following equation.

$$\begin{eqnarray} \displaystyle\frac{{\omega}L}{R}-\displaystyle\frac{1}{{\omega}CR}=-1\\ \\ {\Leftrightarrow}LC{\omega}^2+RC{\omega}-1=0\tag{11} \end{eqnarray}$$

Solving equation (11), the angular frequency ${\omega}$ is expressed by the following equation.

$$\begin{eqnarray} {\omega}=\frac{-RC+\sqrt{(RC)^2+4LC}}{2LC}\tag{12} \end{eqnarray}$$

In the above equation, the root (√) is preceded by "+ (plus)" because ${\omega}{>}0$ is considered. Let ${\omega}$ in equation (12) be ${\omega}_1$.

Therefore, ${\Delta}{\omega}(={\omega}_2-{\omega}_1)$ is expressed by the following equation.

$$\begin{eqnarray} {\Delta}{\omega}&=&{\omega}_2-{\omega}_1\\ \\ &=&\frac{RC+\sqrt{(RC)^2+4LC}}{2LC}-\frac{-RC+\sqrt{(RC)^2+4LC}}{2LC}\\ \\ &=&\frac{R}{L}\tag{13} \end{eqnarray}$$

Note that ${\Delta}{\omega}$ is called Bandwidth. From the above, the Q factor of the RLC series resonant circuit is expressed by the following equation.

$$\begin{eqnarray} Q=\frac{{\omega}_0}{{\Delta}{\omega}}=\frac{{\omega}_0}{{\omega}_2-{\omega}_1}&=&\frac{\displaystyle\frac{1}{\sqrt{LC}}}{\displaystyle\frac{R}{L}}\\ \\ &=&\frac{1}{R}\sqrt{\frac{L}{C}}\tag{14} \end{eqnarray}$$

In addition, using "${\omega}_0=\displaystyle\frac{1}{\sqrt{LC}}$" in equation (14), the following equation is obtained.

$$\begin{eqnarray} Q=\frac{1}{R}\sqrt{\frac{L}{C}}=\frac{{\omega}_0L}{R}=\frac{1}{{\omega}_0CR}\tag{15} \end{eqnarray}$$

This concludes the derivation of the Q factor of the RLC series resonant circuit; let's look at the Q factor in a little more detail.

Since the current flowing in the RLC series resonant circuit at the resonant angular frequency ${\omega}_0$ is $I_{MAX}$, the "magnitude $V_R$ of the voltage across the resistor $R$", the "magnitude $V_L$ of the voltage across the inductor $L$", and the "magnitude $V_C$ of the voltage across the capacitor $C$" are as follows.

$$\begin{eqnarray} V_R&=&R×I_{MAX}\tag{16}\\ \\ V_L&=&{\omega}_0L×I_{MAX}\tag{17}\\ \\ V_C&=&\frac{1}{{\omega}_0C}×I_{MAX}\tag{18} \end{eqnarray}$$

From equations (16) to (18), the Q factor can be transformed as follows.

$$\begin{eqnarray} Q&=&\frac{{\omega}_0L}{R}=\frac{{\omega}_0L×I_{MAX}}{R×I_{MAX}}=\frac{V_L}{V_R}\tag{19}\\ \\ Q&=&\frac{1}{{\omega}_0CR}=\frac{{\omega}_0L×I_{MAX}}{R×I_{MAX}}=\frac{V_C}{V_R}\tag{20} \end{eqnarray}$$

Therefore, the Q factor can be said to be the ratio of "the magnitude $V_R$ of the voltage across the resistor $R$" to "the magnitude $V_L$ of the voltage across the inductor $L$" or "the magnitude $V_C$ of the voltage across the capacitor $C$"

Relationship between "Q factor" and "voltage across the inductor L and capacitor C

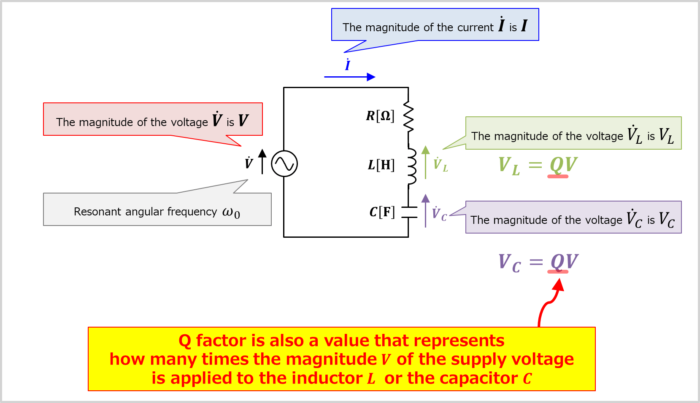
Since the magnitude of the current flowing in the RLC series resonant circuit at the resonant angular frequency ${\omega}_0$ is $I_{MAX}$, the magnitude $V_L$ of the voltage across the inductor $L$ is given by the following equation.

$$\begin{eqnarray} V_L={\omega}_0L×I_{MAX}={\omega}_0L×\frac{V}{R}=\frac{{\omega}_0L}{R}×V=Q×V\tag{21} \end{eqnarray}$$

Similarly, the magnitude $V_C$ of the voltage across the capacitor $C$ is given by the following equation.

$$\begin{eqnarray} V_C=\frac{1}{{\omega}_0C}×I_{MAX}=\frac{1}{{\omega}_0C}×\frac{V}{R}=\frac{1}{{\omega}_0CR}×V=Q×V\tag{22} \end{eqnarray}$$

Therefore, the Q factor is also a value that represents how many times the magnitude $V$ of the supply voltage is applied to the inductor $L$ or the capacitor $C$. The larger the Q factor, the larger the voltage applied to the inductor $L$ and the capacitor $C$.

Summary

This article described the following information about "Q Factor of RLC Series Resonant Circuit".

1. What is the Q factor of RLC series resonant circuit?
2. Derivation of Q factor of RLC series resonant circuit
3. Relationship between "Q factor" and "voltage across the inductor L and capacitor C

Thank you for reading.