Regarding the Pulse Wave: This article will explain the information below.
- How to obtain RMS Value and Average Value
RMS Value and Average Value of Pulse Wave

The first illustration shows the root mean square (RMS) value and average value of a pulse wave (with a maximum value of \(V_M\) and a period of \(T\)).
Now, let's explain how each of these values are calculated (we strive to include as many intermediate steps as possible).
Waveform of a Pulse Wave
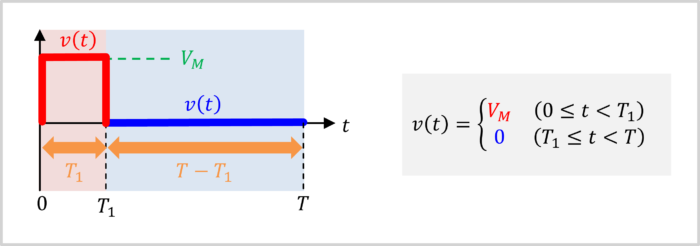
To find the root mean square (RMS) value and average value of a pulse wave, we first need to express the pulse wave as a formula.
The pulse wave has different formulas for the red region \(\left(0 \leq t \lt T_1\right)\) and the blue region \(\left(T_1 \leq t \lt T\right)\).
Let's calculate the formulas for the red region and blue region.
Red Region
The region "\(0 \leq t \lt T_1\)" corresponds to the red region.
The red line is always \(V_M\) during the time \(T_1\).
Therefore, the red region can be represented by the following formula.
\begin{eqnarray}
v(t)=V_M
\end{eqnarray}
Blue Region
The region "\(T_2 \leq t \lt T\)" corresponds to the blue region.
The blue rgsion is zero.
Therefore, the blue region can be represented by the following formula.
\begin{eqnarray}
v(t)=0
\end{eqnarray}
By combining the red region and the blue region, the pulse wave can be represented by the following formula.
\begin{eqnarray}
v(t) = \begin{cases}
V_M & \left(0 \leq t \lt T_1\right) \\
\\
0 & \left(T_1 \leq t \lt T\right)
\end{cases}
\end{eqnarray}
RMS Value of a Pulse Wave
The root mean square (RMS) value \(V_{RMS}\) of a waveform \(v(t)\) is the square root of the mean of the square of \(v(t)\). It can be represented by the following formula:
\begin{eqnarray}
V_{RMS} &=& \sqrt{\displaystyle\frac{1}{T} \displaystyle \int_{0}^{T}v(t)^2dt}
\end{eqnarray}
The red region is \(0 \leq t \lt T_1\)", and the blue region is "\(T_1 \leq t \lt T\)".
In the formula for finding the absolute value, if we separate the red region and the blue region, we get the following formula.
\begin{eqnarray}
V_{RMS} &=& \sqrt{\displaystyle\frac{1}{T} \left(\displaystyle \int_{0}^{T_1}v(t)^2dt+\displaystyle \int_{T_1}^{T}v(t)^2dt\right )}\\
\\
&=& \sqrt{\displaystyle\frac{1}{T} \left(\displaystyle \int_{0}^{T_1}V_M^2dt+\displaystyle \int_{T_1}^{T}0\right )}\\
\\
&=& \sqrt{\displaystyle\frac{1}{T} \displaystyle \int_{0}^{T_1}V_M^2dt}
\end{eqnarray}
\(V_M^2\) is not a variable that changes with time \(t\), but a constant. Therefore, it can be taken out of the integration. As a result, the following equation is obtained.
\begin{eqnarray}
V_{RMS} &=& \sqrt{\displaystyle\frac{1}{T_1} V_M^2\displaystyle \int_{0}^{T}1dt}\\
\\
&=& V_M\sqrt{\displaystyle\frac{1}{T_1} \displaystyle \int_{0}^{T}1dt}
\end{eqnarray}
When calculating the above equation, the following formula is obtained.
\begin{eqnarray}
V_{RMS} &=& V_M\sqrt{\displaystyle\frac{1}{T} \left[t\right]_{0}^{T_1}}\\
\\
&=& V_M\sqrt{\displaystyle\frac{1}{T} \left(T_1-0\right)}\\
\\
&=& \sqrt{\displaystyle\frac{T_1}{T}}V_M
\end{eqnarray}
Therefore, the root mean square (RMS) value \(V_{RMS}\) of the pulse wave is as follows.
\begin{eqnarray}
V_{RMS} =\sqrt{\displaystyle\frac{T_1}{T}}V_M
\end{eqnarray}
Average Value of a Pulse Wave
The average value \(V_{AVE}\) of a waveform \(v(t)\) is the average value of the absolute value \(|v(t)|\) of \(v(t)\) and can be represented by the following formula:
Formula to find the average value
\begin{eqnarray}
V_{AVE} &=& \displaystyle\frac{1}{T} \displaystyle \int_{0}^{T}|v(t)|dt
\end{eqnarray}
This formula for calculating the average value uses the absolute value \(|v(t)|\) of \(v(t)\).
Therefore, if there is a negative region in the waveform, it needs to be converted so that the negative region becomes positive.
In the case of a pulse wave, there is no negative region, so the formula for \(v(t)\) and the formula for the absolute value \(|v(t)|\) of \(v(t)\) become the same.
Therefore, the absolute value \(|v(t)|\) of \(v(t)\) can be represented by the following formula.
\begin{eqnarray}
|v(t)| = \begin{cases}
V_M & \left(0 \leq t \lt T_1\right) \\
\\
0 & \left(T_1 \leq t \lt T\right)
\end{cases}
\end{eqnarray}
In the formula to find the average value, if we separate each term, we get the following formula.
\begin{eqnarray}
V_{AVE} &=& \displaystyle\frac{1}{T} \displaystyle \int_{0}^{T}|v(t)|dt\\
\\
&=& \displaystyle\frac{1}{T} \left(\displaystyle \int_{0}^{T_1}|v(t)|dt+\displaystyle \int_{T_1}^{T}|v(t)|dt\right )\\
\end{eqnarray}
Since the pulse wave is zero in the region \(T_1 \leq t \lt T\), the above equation becomes:
\begin{eqnarray}
V_{AVE} &=& \displaystyle\frac{1}{T} \left(\displaystyle \int_{0}^{T_1}|v(t)|dt+\displaystyle \int_{T_1}^{T}0dt\right )\\
\\
&=&\displaystyle\frac{1}{T} \displaystyle \int_{0}^{T_1}|v(t)|dt\\
\end{eqnarray}
In the above equation, when substituting \(v(t)=V_M\), the following formula is obtained.
\begin{eqnarray}
V_{AVE} &=& \displaystyle\frac{1}{T} \displaystyle \int_{0}^{T_1}V_Mdt\\
\\
&=& \displaystyle\frac{1}{T} V_M\displaystyle \int_{0}^{T_1}1dt\\
\\
&=& \displaystyle\frac{1}{T}V_M \left[t\right]_{0}^{T_1}\\
\\
&=& \displaystyle\frac{1}{T}V_M \left(T_1-0\right)\\
\\
&=&\displaystyle\frac{T_1}{T}V_M
\end{eqnarray}
Therefore, the average value \(V_{AVE}\) of the pulse wave is as follows.
\begin{eqnarray}
V_{AVE} &=& \displaystyle\frac{T_1}{T}V_M
\end{eqnarray}
Summary
In this article, the following information on the "Pulse Wave" was explained.
- How to obtain RMS Value and Average Value
Thank you for reading.