[Half-Wave Rectified Sine-Wave] RMS Value, Average Value, Form Factor, and Crest Factor

Regarding the Half-Wave Rectified Sine-Wave: This article will explain the information below.

• How to obtain RMS Value, Average Value, Form Factor, and Crest Factor

RMS Value, Average Value, Form Factor, and Crest Factor of Half-Wave Rectified Sine-Wave

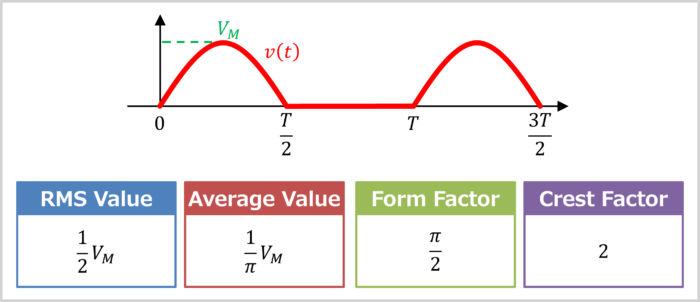
The first illustration shows the root mean square (RMS) value, average value, form factor, and crest factor of a half-wave rectified sine-wave (with a maximum value of \(V_M\) and a period of \(T\)).

Now, let's explain how each of these values are calculated (we strive to include as many intermediate steps as possible).

Waveform of a Half-Wave Rectified Sine-Wave

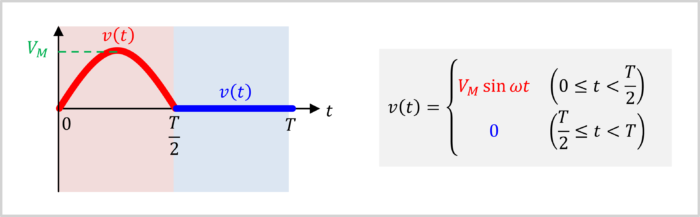
To find the root mean square (RMS) value and average value of a half-wave rectified sine-wave, we first need to express the half-wave rectified sine-wave as a formula.

The half-wave rectified sine-wave has different formulas for the red region \(\left(0 \leq t \lt \displaystyle \frac{T}{2}\right)\) and the blue region \(\left(\displaystyle \frac{T}{2} \leq t \lt T\right)\).

Let's calculate the formulas for the red region and blue region.

Red Region

The region "\(0 \leq t \lt \displaystyle \frac{T}{2}\)" corresponds to the red region.

The red region is part of the waveform of \(V_M\sin{{\omega}t}\).

Therefore, the red region can be represented by the following formula.

\begin{eqnarray}
v(t)=V_M\sin{{\omega}t}
\end{eqnarray}

Blue Region

The region "\(\displaystyle \frac{T}{2} \leq t \lt T\)" corresponds to the blue region.

The blue region is zero.

Therefore, the blue region can be represented by the following formula.

\begin{eqnarray}
v(t)=0
\end{eqnarray}

By combining the red region and the blue region, the half-wave rectified sine-wave can be represented by the following formula.

\begin{eqnarray}
v(t) = \begin{cases}
V_M\sin{{\omega}t} & \left(0 \leq t \lt \displaystyle \frac{T}{2}\right) \\
\\
0 & \left(\displaystyle \frac{T}{2} \leq t \lt T\right)
\end{cases}
\end{eqnarray}

Next, we will calculate the RMS value, average value, form factor, and crest factor of the half-wave rectified sine-wave. However, using the above formula can make the calculation slightly complex.

Therefore, to simplify the calculation this time, we will convert the time axis (horizontal axis \(t\)) to the phase axis (horizontal axis \({{\omega}t}\)).

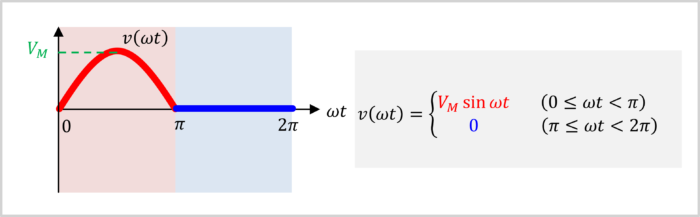
When the time axis (horizontal axis \(t\)) is converted to the phase axis (horizontal axis \({{\omega}t}\)), the half-wave rectified sine-wave becomes the following formula.

\begin{eqnarray}
v({\omega}t) = \begin{cases}
V_M\sin{{\omega}t} & \left(0 \leq {\omega}t \lt \pi\right) \\
\\
0 & \left(\pi \leq {\omega}t \lt 2\pi\right)
\end{cases}
\end{eqnarray}

RMS Value of a Half-Wave Rectified Sine-Wave

The root mean square (RMS) value \(V_{RMS}\) of a waveform \(v({{\omega}t})\) is the square root of the mean of the square of \(v({{\omega}t})\). It can be represented by the following formula:

\begin{eqnarray}
V_{RMS} &=& \sqrt{\displaystyle\frac{1}{2\pi} \displaystyle \int_{0}^{2\pi}v({{\omega}t})^2d({{\omega}t}})
\end{eqnarray}

The red region is \(0 \leq {\omega}t \lt \pi\)", and the blue region is "\(\pi \leq {\omega}t \lt 2\pi\)".

In the formula for finding the absolute value, if we separate the red region and the blue region, we get the following formula.

\begin{eqnarray}
V_{RMS} &=& \sqrt{\displaystyle\frac{1}{2\pi} \left(\displaystyle \int_{0}^{\pi}v({{\omega}t})^2d({\omega}t)+\displaystyle \int_{\pi}^{2\pi}v({{\omega}t})^2d({\omega}t)\right )}\\
\\
&=& \sqrt{\displaystyle\frac{1}{2\pi} \left(\displaystyle \int_{0}^{\pi}(V_M\sin{{\omega}t})^2d({\omega}t)+\displaystyle \int_{\pi}^{2\pi}0^2d({\omega}t)\right )}\\
\\
&=& \sqrt{\displaystyle\frac{1}{2\pi}\displaystyle \int_{0}^{\pi}(V_M\sin{{\omega}t})^2d({\omega}t)}
\end{eqnarray}

The formula for the red region is \(V_M\sin{{\omega}t}\), and the formula for the blue region is \(-V_M\sin{{\omega}t}\), but in the calculation of the effective value, we square it, so we can combine the above formulas. If we combine them, we get the following formula.

\begin{eqnarray}
V_{RMS} &=& \sqrt{\displaystyle\frac{1}{\pi} \displaystyle \int_{0}^{2\pi}(V_M\sin{{\omega}t})^2d({\omega}t)}
\end{eqnarray}

In the above formula, if you let

\begin{eqnarray}
X &=& \displaystyle \int_{0}^{\pi}(V_M\sin{{\omega}t})^2 d({\omega}t)
\end{eqnarray}

then the root mean square (RMS) value \(V_{RMS}\) of a waveform \(v({{\omega}t})\) can be represented by the following formula:

\begin{eqnarray}
V_{RMS} &=& \sqrt{\displaystyle\frac{1}{2\pi} X}
\end{eqnarray}

Next, we calculate the value of \(X\).

\begin{eqnarray}
X &=& \displaystyle \int_{0}^{\pi}v({{\omega}t})^2 d({\omega}t)\\
\\
&=& \displaystyle \int_{0}^{\pi}{V_M}^2{\sin}^2{\omega}t d({\omega}t)\\
\\
&=& {V_M}^2\displaystyle \int_{0}^{\pi}{\sin}^2{\omega}t d({\omega}t)\\
\\
&=& {V_M}^2\displaystyle \int_{0}^{\pi}\displaystyle \frac{1-{\cos2{\omega}t}}{2} d({\omega}t)\\
\\
&=& {V_M}^2 \left[\displaystyle\frac{1}{2}{{\omega}t}-\frac{1}{4}{\sin2{\omega}t} \right]_{0}^{\pi}\\
\\
&=& {V_M}^2 \left( \displaystyle\frac{1}{2}×{\pi}-\frac{1}{4}{\sin{2\pi}}\right)\\
\\
&=& \displaystyle\frac{{V_M}^2 {\pi}}{2}
\end{eqnarray}

Therefore, the root mean square (RMS) value \(V_{RMS}\) of a waveform \(v({{\omega}t})\) becomes:

\begin{eqnarray}
V_{RMS} &=&\sqrt{\displaystyle\frac{1}{2\pi} X}\\
\\
&=&\sqrt{\displaystyle\frac{1}{2\pi} \displaystyle\frac{{V_M}^2 {\pi}}{2}}\\
\\
&=&\displaystyle\frac{1}{2}V_M
\end{eqnarray}

Average Value of a Half-Wave Rectified Sine-Wave

The average value \(V_{AVE}\) of a waveform \(v({{\omega}t})\) is the average value of the absolute value \(|v({{\omega}t})|\) of \(v({{\omega}t})\) and can be represented by the following formula:

This formula for calculating the average value uses the absolute value \(|v({{\omega}t})|\) of \(v({{\omega}t})\).

Therefore, if there is a negative region in the waveform, it needs to be converted so that the negative region becomes positive.

In the case of a half-wave rectified sine-wave, there is no negative region, so the formula for \(v({{\omega}t})\) and the formula for the absolute value \(|v({{\omega}t})|\) of \(v({{\omega}t})\) become the same.

Therefore, the absolute value \(|v({{\omega}t})|\) of \(v({{\omega}t})\) can be represented by the following formula.

\begin{eqnarray}
|v({{\omega}t})| = \begin{cases}
V_M\sin{{\omega}t} & \left(0 \leq {\omega}t \lt \pi\right) \\
\\
0 & \left(\pi \leq {\omega}t \lt 2\pi\right)
\end{cases}
\end{eqnarray}

In the formula to find the average value, if we separate each term, we get the following formula.

\begin{eqnarray}
V_{AVE} &=& \displaystyle\frac{1}{2\pi} \displaystyle \int_{0}^{2\pi}|v({\omega}t)|d({{\omega}t})\\
\\
&=& \displaystyle\frac{1}{2\pi}\left(\displaystyle \int_{0}^{\pi}|v({\omega}t)|d({{\omega}t})+ \int_{\pi}^{2\pi}|v({\omega}t)|d({{\omega}t}) \right)\\
\end{eqnarray}

Since the half-wave rectified sine-wave is zero in the region \(\pi \leq {\omega}t \lt 2\pi\), the above equation becomes:

\begin{eqnarray}
V_{AVE} &=& \displaystyle\frac{1}{2\pi}\displaystyle \int_{0}^{\pi}|v({\omega}t)|d({{\omega}t})
\end{eqnarray}

If we calculate the above formula, the average value \(V_{AVE}\) of the half-wave rectified sine-wave becomes:

\begin{eqnarray}
V_{AVE} &=& \displaystyle\frac{1}{2\pi}\displaystyle \int_{0}^{\pi}V_M\sin{{\omega}t}d({{\omega}t})\\
\\
&=& \displaystyle\frac{1}{2\pi}V_M\left[-\cos{\omega}t \right]_{0}^{\pi}\\
\\
&=& \displaystyle\frac{V_M}{2\pi}\left(-\cos\pi + \cos0 \right)\\
\\
&=& \displaystyle\frac{1}{\pi}V_M
\end{eqnarray}

Form Factor of a Half-Wave Rectified Sine-Wave

The form factor can be represented by the following formula:

\begin{eqnarray}
\mbox{Form Factor} &=& \displaystyle\frac{\mbox{Root Mean Square Value}~~V_{RMS}}{\mbox{Average Value}~~V_{AVE}}
\end{eqnarray}

Since we've already calculated the root mean square (RMS) value \(V_{RMS}\) and average value \(V_{AVE}\) of the sine wave, we can substitute these values into the formula to calculate the form factor of the half-wave rectified sine-wave.

\begin{eqnarray}
\mbox{Form Factor} = \displaystyle\frac{\displaystyle\frac{1}{2}V_M}{\displaystyle\frac{1}{\pi}V_M} = \displaystyle\frac{\pi}{2}
\end{eqnarray}

Maximum Value of a Half-Wave Rectified Sine-Wave

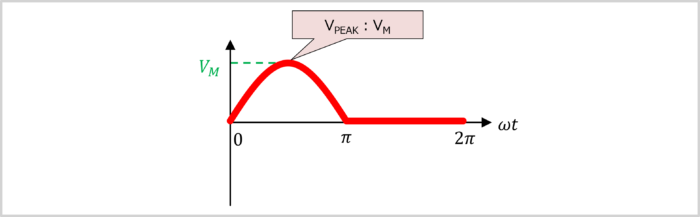
As can be seen from the waveform, the maximum value \(V_{PEAK}\)​ of a half-wave rectified sine-wave is represented by the following value:

\begin{eqnarray}
\mbox{Maximum Value}~~V_{PEAK}=V_M
\end{eqnarray}

Crest Factor of a Half-Wave Rectified Sine-Wave

The Crest factor can be represented by the following formula:

\begin{eqnarray}
\mbox{Crest Factor} &=& \displaystyle\frac{\mbox{Peak Value}~~V_{PEAK}}{\mbox{Root Mean Square Value}~~V_{RMS}}
\end{eqnarray}

Since we've already calculated the root mean square (RMS) value \(V_{RMS}\) and peak value \(V_{PEAK}\) of the sine wave, we can substitute these values into the formula to calculate the peak factor (crest factor) of the half-wave rectified sine-wave.

The Crest factor of the half-wave rectified sine-wave is represented by the following value:

\begin{eqnarray}
\mbox{Crest Factor} = \displaystyle\frac{V_M}{\displaystyle\frac{1}{2}V_M} = 2
\end{eqnarray}

Summary

In this article, the following information on the "Half-Wave Rectified Sine-Wave" was explained.

• How to obtain RMS Value, Average Value, Form Factor, and Crest Factor

Thank you for reading.