Difference between "Average Value" and "RMS Value"

This article will explain the differences between "Average Value" and "RMS Value".

Difference between "Average Value" and "RMS Value"

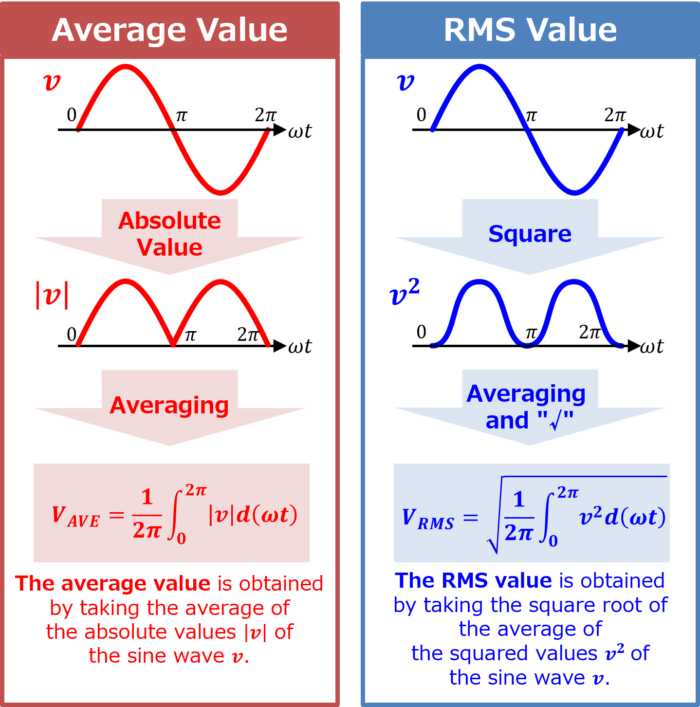
First, let's briefly explain the difference between "Average Value" and "RMS Value" (we will explain each in detail later).

Taking the sine wave \(v=V_M\sin{{\omega}t}\) as an example:

Average Value

The average value is what you get when you replace "negative" values with "positive" ones and take the average. In other words, the average value, \(V_{AVE}\), is the average of the absolute value \(|v|\) of the sine wave \(v\).

For example, in the case of the above figure, the average value \(V_{AVE}\) is represented by the following value:

\begin{eqnarray}
V_{AVE} &=& \displaystyle\frac{1}{2\pi} \displaystyle \int_{0}^{2\pi}|v|d({{\omega}t})\\
\\
&=&\displaystyle\frac{2V_M}{\pi}
\end{eqnarray}

RMS Value

The RMS value is what you get when you take the square root (\(\sqrt{}\)) of the average value of the squared sine wave \(v^2\).

For example, in the case of the above figure, the RMS value \(V_{RMS}\) is represented by the following value:

\begin{eqnarray}
V_{RMS} &=& \sqrt{\displaystyle\frac{1}{2\pi} \displaystyle \int_{0}^{2\pi}v^2d({{\omega}t}})\\
\\
&=&\displaystyle\frac{V_M}{\sqrt{2}}
\end{eqnarray}

Please refer to the following article for the derivation of the above formula. It explains in detail why the average value \(V_{AVE}\) of the sine wave becomes \(\displaystyle\frac{2V_M}{\pi}\), and why the RMS value \(V_{RMS}\) of the sine wave becomes \(\displaystyle\frac{V_M}{\sqrt{2}}\).

: [Sine Wave] RMS Value, Average Value, Form Factor, and Crest Factor
続きを見る

Average Value

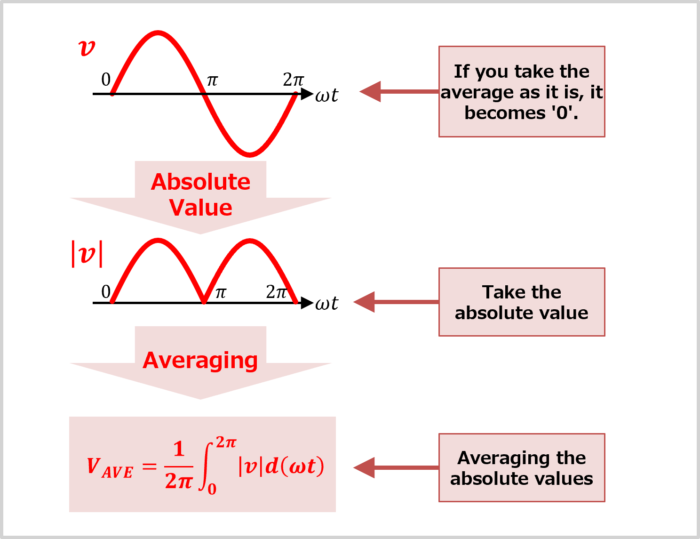
Let's consider the sine wave \(v=V_M\sin{{\omega}t}\) as an example.

Since the average of the 'positive' and 'negative' of AC becomes '0', the average value \(V_{AVE}\) is the average of the absolute value \(|v|\) of the sine wave \(v\). Therefore, the formula to calculate the average value \(V_{AVE}\) is represented by the following formula.

\begin{eqnarray}
V_{AVE} &=& \displaystyle\frac{1}{2\pi} \displaystyle \int_{0}^{2\pi}|v|d({{\omega}t})\\
\\
&=&\displaystyle\frac{2V_M}{\pi}
\end{eqnarray}

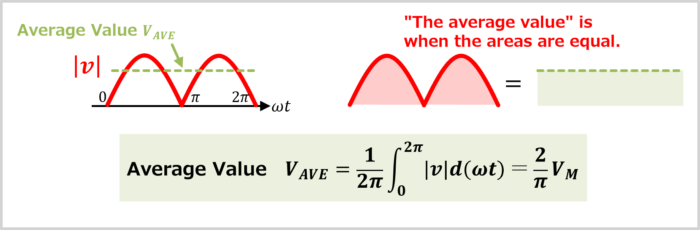
As shown in the following figure, the above formula simply indicates that the areas are equal.

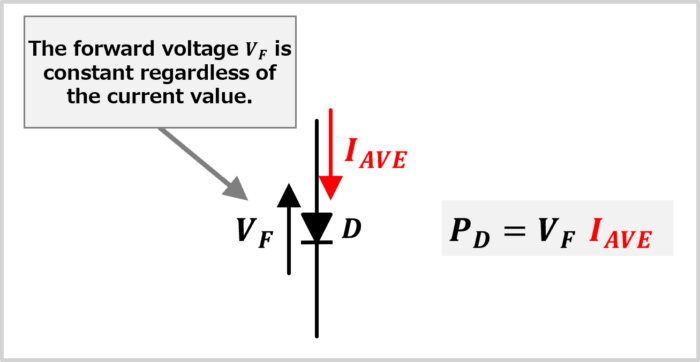
Supplement

The average value \(V_{AVE}\) is used when calculating losses (power consumption) for things where voltage remains constant regardless of the current (such as the forward voltage of a diode).

For example, if the average value of the current flowing through a diode with a forward voltage \(V_{F}\) is \(I_{AVE}\), the loss (power consumption) \(P_{D}\) at the diode is represented by the following formula.

\begin{eqnarray}
P_{D} &=& V_{F} I_{AVE}
\end{eqnarray}

RMS Value

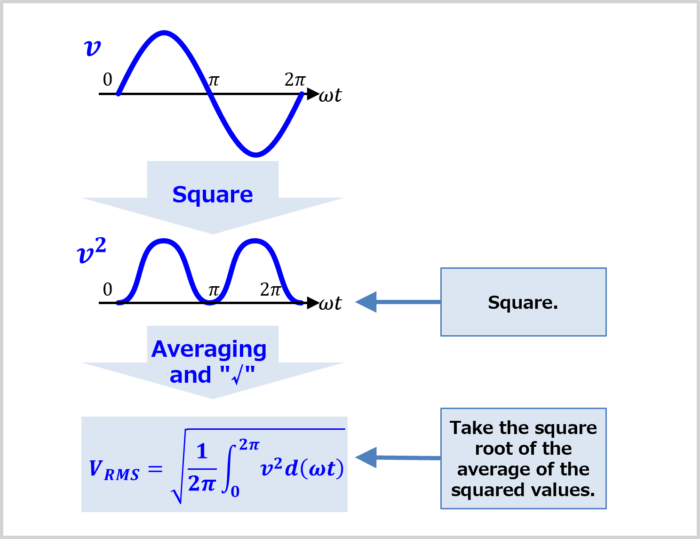
Let's consider the sine wave \(v=V_M\sin{{\omega}t}\) as an example.

The RMS value \(V_{RMS}\) is what you get when you take the square root (\(\sqrt{}\)) of the average value of the squared sine wave \(v^2\).

Therefore, the formula to calculate the RMS value \(V_{RMS}\) is represented by the following formula.

\begin{eqnarray}
V_{RMS} &=& \sqrt{\displaystyle\frac{1}{2\pi} \displaystyle \int_{0}^{2\pi}v^2d({{\omega}t}})\
\end{eqnarray}

But why does it turn out to be this formula?

This is because the RMS value is the "value of the voltage that generates the same power when a DC voltage is applied to the resistance" (it's a bit complicated...).

To explain it in an easy-to-understand way, let's take a square wave v as an example, with a peak value \(V_M\) of \(1{\mathrm{[V]}}\) and a duty ratio \(D\) of \(0.5\).

RMS Value \(V_{RMS}\) of Square Wave \(v\)

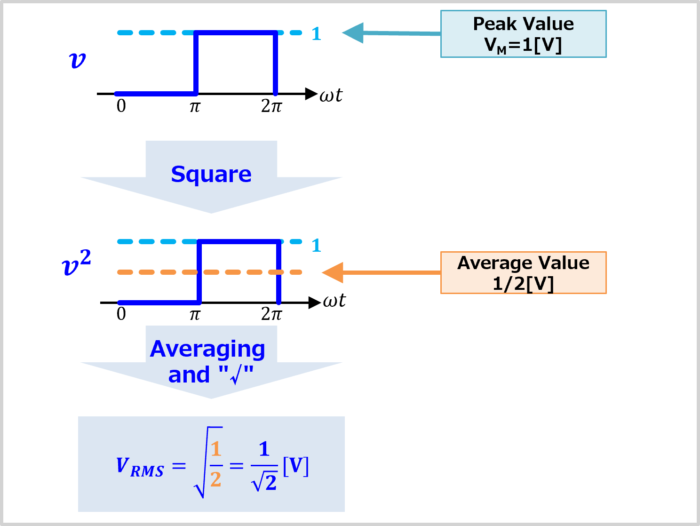
First, let's calculate the RMS value \(V_{RMS}\) of the square wave \(v\).

When you square the square wave \(v\), the first half of the period becomes \(0{\mathrm{[V]}}\) and the second half of the period becomes \(1{\mathrm{[V]}}\).

Therefore, the average value of the squared square wave \(v^2\) is \(\displaystyle\frac {1}{2}{\mathrm{[V]}}\).

Take the square root (\(\sqrt{}\)) of this average value results in \(\displaystyle\frac {1}{\sqrt{2}}{\mathrm{[V]}}\).

In other words, the RMS value \(V_{RMS}\) of the square wave \(v\), with a peak value \(V_M\) of \(1{\mathrm{[V]}}\) and a duty ratio \(D\) of \(0.5\), is \(\displaystyle\frac {1}{\sqrt{2}}{\mathrm{[V]}}\).

Power When Square Wave \(v\) is applied to Resistance \(R\)

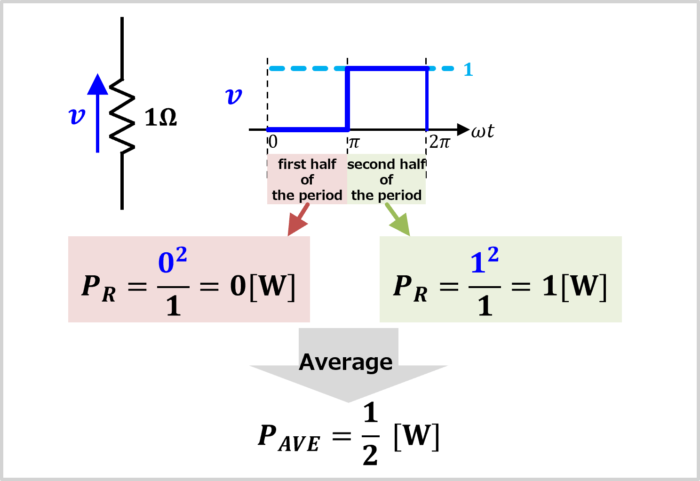
Next, let's calculate the power when the square wave \(v\) is applied to the resistance.

Consider the power \(P_R\) when a square wave \(v\), with a peak value \(V_M\) of \(1{\mathrm{[V]}}\) and a duty ratio \(D\) of \(0.5\), is applied to a resistance \(R\) of \(1Ω\).

The power consumed during the first half of \(0{\mathrm{[V]}}\) period is as follows:

\begin{eqnarray}
P_R=\frac{V^2}{R}=\frac{0^2}{1}=0{\mathrm{[W]}}
\end{eqnarray}

The power consumed during the second half of \(1{\mathrm{[V]}}\) period is as follows:

\begin{eqnarray}
P_R=\frac{V^2}{R}=\frac{1^2}{1}=1{\mathrm{[W]}}
\end{eqnarray}

Therefore, the average power \(P_{AVE}\) is given by the following formula:

\begin{eqnarray}
P_{AVE}=\displaystyle\frac {1}{2}{\mathrm{[W]}}
\end{eqnarray}

Power When DC Voltage \(V\) is Applied to Resistance \(R\)

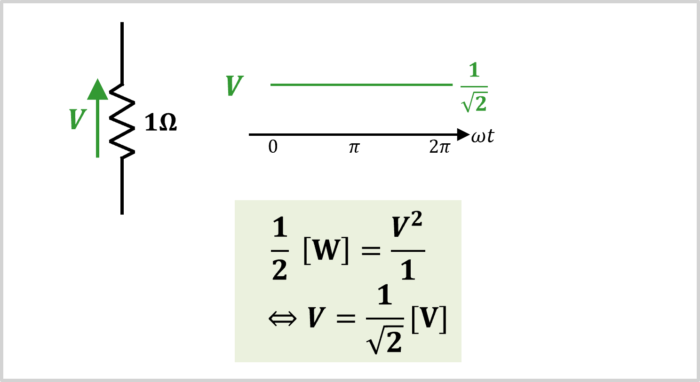
Here, consider the case when the power becomes \(\displaystyle\frac {1}{2}{\mathrm{[W]}}\) when a DC voltage \(V\) is applied to a resistance \(R\) of \(1Ω\). The following equation holds:

\begin{eqnarray}
\displaystyle\frac {1}{2}{\mathrm{[W]}}&=&\frac{V^2}{1}\\
\\
{\Leftrightarrow}V&=&\displaystyle\frac {1}{\sqrt{2}}{\mathrm{[V]}}
\end{eqnarray}

You can see that this matches the RMS value \(V_{RMS}\) that we calculated earlier.

From the above, it can be understood that the RMS value \(V_{RMS}\) is the value of the voltage that generates the same power as when a DC voltage \(V\) is applied to the resistance.

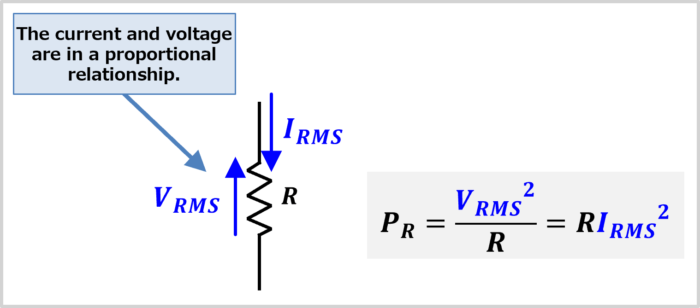
Using RMS Value When Calculating Resistance Load Loss

The RMS value is used when voltage and current are proportional, i.e., when calculating the loss (power consumption) of a resistive load.

For example, if the average value of the voltage applied to a resistance \(R\) is \(V_{RMS}\) and the RMS value of the current flowing at that time is \(I_{RMS}\), the loss (power consumption) \(P_{R}\) at the resistance is given by the following formula:

\begin{eqnarray}
P_{R}=\displaystyle\frac {{V_{RMS}}^2}{R}=R{I_{RMS}}^2
\end{eqnarray}

Using RMS Value When Calculating Resistance Load Loss

Summary

In this article, the following information on the "Average Value" and "RMS Value" was explained.

The difference between "Average Value" and "RMS Value"

Thank you for reading.