Regarding the Resistor, this article will explain the information below.
- Resistance Temperature Characteristics
- Temperature Coefficient of Resistance
Resistance Temperature Characteristics
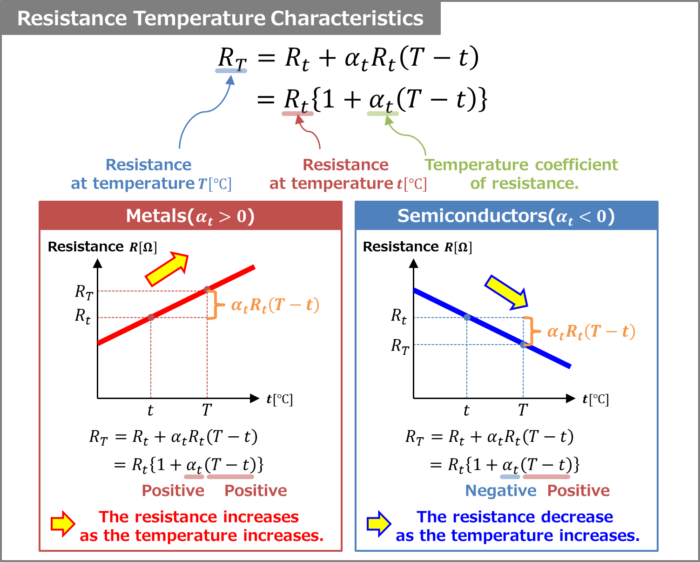
In general, the resistance of metals increases with increasing temperature, while the resistance of semiconductors decreases with increasing temperature.
This change in resistance with temperature can be calculated using the temperature coefficient of resistance \(α_t\), which can be expressed by the following equation:
\begin{eqnarray}
R_T&=&R_t+α_tR_t(T-t)\\
\\
&=&R_t\left\{1+α_t(T-t)\right\}\tag{1}
\end{eqnarray}
, where \(R_T\), \(R_t\), and \(α_t\) indicate the following:
- \(R_T\):Resistance at temperature \(T{\mathrm{[℃]}}\), units of \({\mathrm{[Ω]}}\).
- \(R_t\):Resistance at temperature \(t{\mathrm{[℃]}}\), units of \({\mathrm{[Ω]}}\).
- \(α_t\):Temperature coefficient of resistance.
In equation (1), the resistance \(R_t{\mathrm{[Ω]}}\) is obtained when the temperature changes from \(t{\mathrm{[℃]}}\) to \(T{\mathrm{[℃]}}\).
"\(T-t\)" indicates "how much the temperature has changed with respect to the temperature \(t{\mathrm{[℃]}}\)." If the temperature increases, \(T-t{\;}{\gt}{\;}0\), and if the temperature decreases, \(T-t{\;}{\lt}{\;}0\).
The temperature coefficient of resistance \(α_t\) indicates "how much the resistance changes when the resistance of \(1{\mathrm{[Ω]}}\) rises by \(1{\mathrm{[℃]}}\).
The temperature coefficient of resistance \(α_t\) has positive and negative values and depends on the substance as shown below.
- In the case of metals such as gold, silver, copper, and iron.
- The temperature coefficient of resistance \(α_t\) is positive.
- In the case of "semiconductors such as germanium," "insulators," and "carbon”.
- The temperature coefficient of resistance \(α_t\) is negative.
For example, the temperature coefficient of resistance \(α_t\) of copper is positive and its value is 0.00393.
In the case of metals, since the temperature coefficient of resistance \(α_t\) is positive, if the temperature rises from \(t{\mathrm{[℃]}}\), "\(R_tα_t(T-t)\)" will also be positive. Therefore, the value obtained by adding "\(R_tα_t(T-t)\)" to the resistance value \(R_t{\mathrm{[Ω]}}\) at the temperature \(t{\mathrm{[℃]}}\) is the resistance value \(R_T{\mathrm{[Ω]}}\) at the temperature \(T{\mathrm{[℃]}}\).
On the other hand, in the case of semiconductors, since the temperature coefficient of resistance \(α_t\) is negative, "\(R_tα_t(T-t)\)" becomes negative if the temperature increases from \(t{\mathrm{[℃]}}\). Therefore, resistance \(R_T{\mathrm{[Ω]}}\) at temperature \(T{\mathrm{[℃]}}\) is smaller than resistance \(R_t{\mathrm{[Ω]}}\) at temperature \(t{\mathrm{[℃]}}\).
Exercise
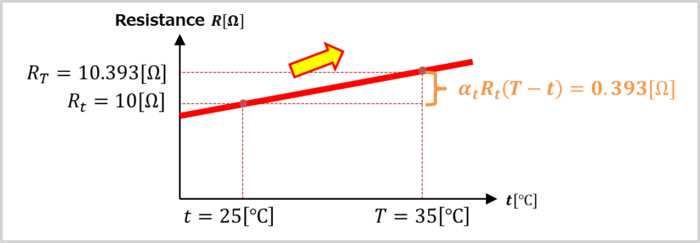
At temperature \(t=25{\mathrm{[℃]}}\), the resistance \(R_t\) of copper was \(10{\mathrm{[Ω]}}\). What is the resistance \(R_T\) of this copper when the temperature rises to \(T=35{\mathrm{[℃]}}\)? Assume that the temperature coefficient of resistance \(α_t\) of copper is 0.00393.
Substituting each value into equation (1), we can obtain the resistance value \(R_T\) when the temperature rises to \(T=35{\mathrm{[℃]}}\).
\begin{eqnarray}
R_T&=&R_t\left\{1+α_t(T-t)\right\}\\
\\
&=&10\left\{1+0.00393(35-25)\right\}\\
\\
&=&10\left\{1+0.00393×10\right\}\\
\\
&=&10\left\{1+0.0393\right\}\\
\\
&=&10×1.0393\\
\\
&=&10.393{\mathrm{[Ω]}}
\end{eqnarray}
From the above equation, it can be seen that as the temperature increases from \(25{\mathrm{[℃]}}\) to \(35{\mathrm{[℃]}}\), the resistance value increases by \(0.393{\mathrm{[Ω]}}\). This is shown in the graph below.
ポイント
- The equation for variation of resistance with temperature
\begin{eqnarray}
R_T&=&R_t+α_tR_t(T-t)\\
\\
&=&R_t\left\{1+α_t(T-t)\right\}
\end{eqnarray} - In the case of metals
- Since the temperature coefficient of resistance \(α_t\) is positive, the resistance value increases as the temperature increases.
- In the case of semiconductors
- Since the temperature coefficient of resistance \(α_t\) is negative, the resistance value decrease as the temperature increases.
What is Temperature Coefficient of Resistance
Transforming equation (1), the resistance temperature coefficient \(α_t\) can be expressed as:
\begin{eqnarray}
α_t=\frac{1}{R_t}×\frac{R_T-R_t}{T-t}{\mathrm{[1/℃]}}
\end{eqnarray}
The temperature coefficient of resistance \(α_t\) indicates "how much the resistance changes when the resistance of \(1{\mathrm{[Ω]}}\) rises by \(1{\mathrm{[℃]}}\).
Therefore, \(α_tR_t\) represents "how much the resistance changes when the resistance of \(R_t{\mathrm{[Ω]}}\) rises by \(1{\mathrm{[℃]}}\)", and \(α_tR_t\) indicates the slope of the temperature change in resistance.
The temperature coefficient of resistance \(α_t\) varies depending on the substance. The table below shows the temperature coefficient of resistance αt at temperature \(t=20{\mathrm{[℃]}}\).
| Substance | \(α_t{\mathrm{[1/℃]}}\) | ||
| Conductor | Copper | Cu | 0.00393 |
| Silver | Ag | 0.00380 | |
| Gold | Au | 0.00340 | |
| Iron | Fe | 0.00500 | |
| Nichrome | - | 0.00019 | |
| Nickel | Ni | 0.00600 | |
| Aluminum | Al | 0.00390 | |
| Bismuth | Bi | 0.00400 | |
| Cadmium | Cd | 0.00380 | |
| Mercury | Hg | 0.00089 | |
| Magnesium | Mg | 0.00400 | |
| Molybdenum | Mo | 0.00330 | |
| Lead | Pb | 0.00390 | |
| Palladium | Pd | 0.00330 | |
| Platinum | Pt | 0.00300 | |
| Tin | Sn | 0.00420 | |
| Tungsten | W | 0.00450 | |
| zinc | Zn | 0.00370 | |
| Semiconductor & Others | Germanium | Ge | -0.05000 |
| Silicon | Si | -0.08000 | |
| Saturated saline solution | - | -0.00500 | |
Copper, which is often used as a conductor, has a lower temperature coefficient of resistance \(α_t\) than iron. Nichrome is also used for electric heating wire because of its resistance to temperature change.
Supplement
- The Temperature Coefficient of Resistance is sometimes referred to as "TCR.
- The unit of resistance temperature coefficient is not only \({\mathrm{[1/℃]}}\), but also \({\mathrm{[{\%}/℃]}}\) or \({\mathrm{[ppm/℃]}}\) in some cases. In this case, the following equation can be used for calculation.
\begin{eqnarray}
α_t&=&\frac{1}{R_t}×\frac{R_T-R_t}{T-t}{\mathrm{[1/℃]}}\\
\\
&=&\frac{1}{R_t}×\frac{R_T-R_t}{T-t}×100{\mathrm{[{\%}/℃]}}\\
\\
&=&\frac{1}{R_t}×\frac{R_T-R_t}{T-t}×10^6{\mathrm{[ppm/℃]}}\\
\end{eqnarray}
Summary
This article described the following information about "Resistor".
- Resistance Temperature Characteristics
- Temperature Coefficient of Resistance
Thank you for reading.