When current flows (voltage is applied) to a resistor, the temperature of the resistor rises.
The temperature rise of a resistor depends on the rated power of the resistor.
Regarding the Resistor, this article will explain the information below.
- Resistor Temperature Rise Calculation
- Heat Dissipated by Resistor
Resistor Temperature Rise Calculation
When current flows (voltage is applied) to a resistor, the temperature of the resistor rises.
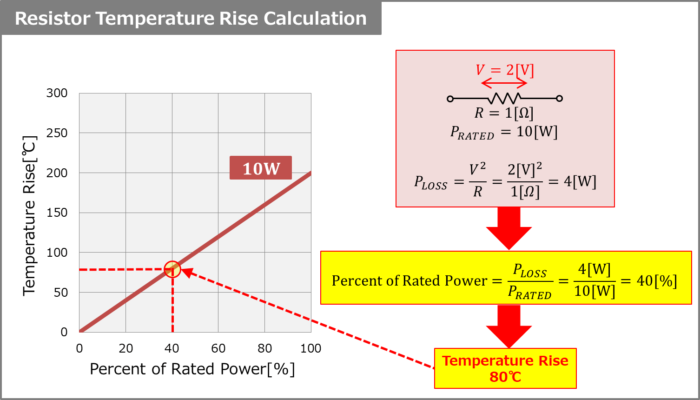
The temperature rise of the resistor is indicated by the graph of Temperature rise vs Power dissipation on the data sheet.
The vertical axis of the graph is the Percent of Rated Power, and the horizontal axis is the Temperature Rise.
The Percent of Rated Power on the horizontal axis represents the power consumption PLOSS relative to the rated power PRATED and is expressed by the following equation:
\begin{eqnarray}
\mbox{Percent of Rated Power}=\frac{\mbox{Power Consumption}{\;}P_{LOSS}}{\mbox{Rated Power}{\;}P_{RATED}}{\mathrm{[{\%}]}}
\end{eqnarray}
For example, assume that the graph of Temperature rise vs Power dissipation for a resistor (R=1Ω, rated power PRATED=10W) is as shown above. If the voltage across this resistor is 2V, the power consumption PLOSS of the resistor is the following value:
\begin{eqnarray}
P_{LOSS}=\frac{V^2}{R}=\frac{2{\mathrm{[V]}}^2}{1{\mathrm{[{\Omega}]}}}=4{\mathrm{[W]}}
\end{eqnarray}
Therefore, the Percent of Rated Power is the following value:
\begin{eqnarray}
\mbox{Percent of Rated Power}=\frac{\mbox{Power Consumption}{\;}P_{LOSS}}{\mbox{Rated Power}{\;}P_{RATED}}=\frac{4{\mathrm{[W]}}}{10{\mathrm{[W]}}}=40{\mathrm{[{\%}]}}
\end{eqnarray}
In the graph of Temperature rise vs Power dissipation shown above, if the Percent of Rated Power is 40%, the surface temperature of the resistor will increase by 80°C.
If the ambient temperature of the resistor is 25°C, the surface temperature of the resistor is the following value:
\begin{eqnarray}
25{\mathrm{[℃]}}+80{\mathrm{[℃]}}=105{\mathrm{[℃]}}
\end{eqnarray}
If the resistor is in an enclosure and the ambient temperature of the resistor is 50°C, the surface temperature of the resistor is the following value:
\begin{eqnarray}
50{\mathrm{[℃]}}+80{\mathrm{[℃]}}=130{\mathrm{[℃]}}
\end{eqnarray}
The higher the rated power of the resistor, the greater the temperature rise.
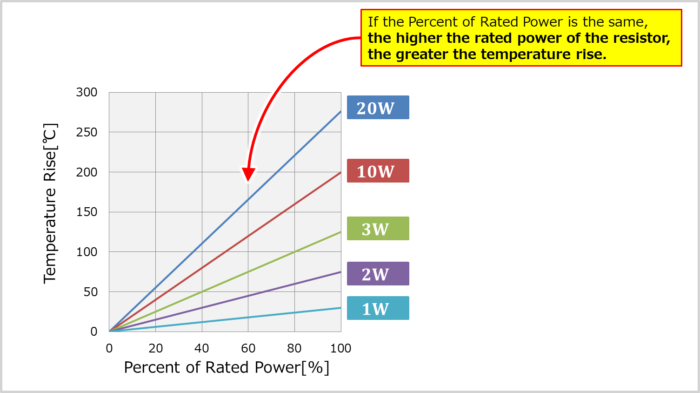
The graph of Temperature rise vs Power dissipation is different for different rated power and types of resistors.
The graph of Temperature rise vs Power dissipation for various resistors with different rated power is shown above.
If the Percent of Rated Power is the same, the higher the rated power of the resistor, the greater the temperature rise.
Therefore, the concept of temperature rise is different for "Resistors with low-rated power" and "Resistors with high-rated power.
- Resistors with low-rated power
- Since the temperature rise is small, the design should mainly consider the rated power, and the temperature rise of the resistor does not need to be that much of a concern.
- Resistors with high-rated power
- Since the temperature rise is large, the design should consider the temperature rise as well as the rated power. In addition, consider whether or not the resistor needs to be floated off the board to account for the temperature rise.
Supplement
Use caution when placing heat-sensitive components near the resistor.
For example, electrolytic capacitors have upper operating temperature limits (85°C and 105°C). Therefore, be careful when placing resistors near electrolytic capacitors.
Heat Dissipated by Resistor
This section describes how to reduce the temperature rise of resistors.
Chip resistor only
- Increase the size of the lands where chip resistors are mounted.
- Increase the pattern width connected to the land.
Chip and lead resistors
- Select resistors by considering derating against the power dissipation of the resistor.
- Use resistors with heat dissipation measures.
Summary
This article described the following information about "Resistor".
- Resistor Temperature Rise Calculation
- Heat Dissipated by Resistor
Thank you for reading.